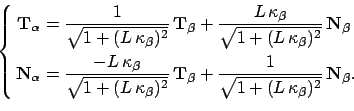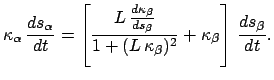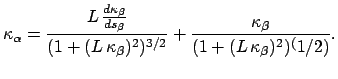We now derive relations between the curvature of the front-tire
track and the back-tire track to help us construct the initial back
tire track segment, and define the differential equation used to extend
the tracks. But first, to distinguish between the information for
each curve, we will use subscripts. For instance, we will use
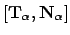
for the Frenet frame of

and
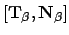
for the Frenet frame of
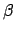
.
The derivations of the relations between the curvatures of the front
and back tire tracks are based on differentiating the fundamental relation
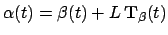 , ,
|
(1) |
and using the Frenet frame equations to provide a method for differentiating
the unit tangent vector and the unit normal vector of a curve. Differentiating
(1) with respect to
 and using the chain rule, we have that
where
and using the chain rule, we have that
where
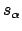
and

are the arclength parameters of the front-tire track and the back-tire track
respectively. The orthogonality of the unit tangent and the unit normal vectors of
the back tire track implies
This implies that
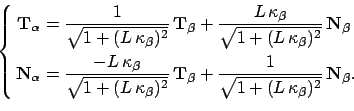 |
(2) |
which relates the Frenet frames of the front and back tire tracks through the curvature
of the back tire track.
Differentiating the equation for the unit tangent vector of the front tire track
in (2) with respect to
 and using the Frenet frame equations for the front and back tire tracks,
we have that
and using the Frenet frame equations for the front and back tire tracks,
we have that
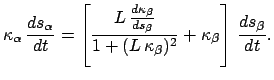 |
(3) |
by equating the coefficients of
 in both sides of the equation Furthermore, using the relation between
in both sides of the equation Furthermore, using the relation between
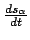 and
and
 ,
we have that
,
we have that
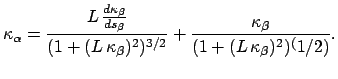 |
(4) |
Notice that (3) and (4)
imply that the curvature
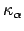 of the front-tire track depends only on the curvature
of the front-tire track depends only on the curvature
 of the back-tire track.
of the back-tire track.
The importance of (3) and (4)
is that knowing the curvature of the front tire we may solve for the curvature
of the back tire by viewing them as a differential equations. However, as a
differential equation to solve for
 it presents some problems. These equations are highly nonlinear and the curvature of
the front tire track is not naturally given in terms of back tire track. We can
overcome these difficulties by introducing alternative
variables that are naturally associated to riding bicycles.
it presents some problems. These equations are highly nonlinear and the curvature of
the front tire track is not naturally given in terms of back tire track. We can
overcome these difficulties by introducing alternative
variables that are naturally associated to riding bicycles.