Which Way Did You Say
That Bicycle Went? 		David L. Finn
Rose-Hulman
Institute of Technology

Problem Statement I

Problem Statement II
Solution to Original
Problem

Outline of Construction
of Ambiguous Tracks

Animations and Examples
of Ambiguous Tracks

Geometry of Tire Tracks

Part I of Solution:
Creating an Initial
Piece of Track

Part II of Solution
Extending the Track

References
Geometry of Bicycle Tracks

We use a geometric view of bicycle tracks, and how they are created to construct ambiguous tire tracks. This is the same approach used in Can a Bicycle Create a Unicycle Track? to describe the creation of a unicycle track with a bicycle. The geometric relations governing the creation or bicycle tracks are obtained by differentiating the fundamental relation between the front and back tire tracks

.

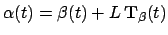
In order to state these relations, we use some elementary differential geometry (curvature, Frenet frames, and the fundamental theorem of plane curves). Most of the differential geometry that we require can be found in calculus textbooks or undergraduate texts on differential geometry, see the references.

The main tools that we use to describe the geometry of tire tracks are the Frenet frames of the tire tracks and the unsigned curvature of each tire track. The Frenet frame of a plane curve is the pair of unit vectors

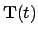
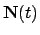
$ \mathbf{ T}(t)$ (the unit tangent vector) and $ \mathbf{ N}(t)$ (the unit normal vector),
where 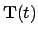$ \mathbf{ T}(t)$ is defined by the convention that if
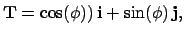
then
The importance of the Frenet frame is that the geometry of the curve is given by how the Frenet frame changes. Specifically, the signed curvature $ \kappa$ of the curve is given by the Frenet frame equations,
$\displaystyle \frac{d\mathbf{T}}{ds} = \kappa\,\mathbf{N} \quad\hbox{and}\quad \frac{d\mathbf{N}}{ds} = -\kappa\,\mathbf{T}$
where is the arclength parameter of the curve. We note the Frenet frame equations can also be written using the chain rule as
where we view as time and as the speed of the particle creating the curve. The signed curvature as defined above is different from the curvature of a curve as usually defined in standard calculus texts. The unsigned curvature
is the curvature defined in most calculus texts, and can be shown to be the reciprocal of the radius of the best fit circle to the curve at a point. The importance of the signed curvature that we will exploit is that the signed curvature determines the curve up to a translation and a rotation. This important fact is known in differential geometry as the fundamental theorem of plane curves.