Which Way Did You Say
That Bicycle Went? 		David L. Finn
Rose-Hulman
Institute of Technology

Problem Statement I

Problem Statement II
Solution to Original
Problem

Outline of Construction
of Ambiguous Tracks

Animations and Examples
of Ambiguous Tracks

Geometry of Tire Tracks

Part I of Solution:
Creating an Initial
Piece of Track

Part II of Solution
Extending the Track

References
Outline of the Construction
of Ambiguous Tracks

To construct ambiguous tracks, tire tracks where you can not determine which direction the bicycle was travelling, we simply look at the method for determining the direction and define a track where it won't work. For instance, we can not use the method described above: given a back-tire track 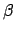$\beta$ with the front-tire track described as either

$ \beta(t)+L\,\mathbf{ T}_\beta(t)$ or $ \beta(t) - L\,\mathbf{ T}_\beta(t)$.
This means that one method for creating ambiguous tire tracks is to create a back tire track 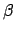$\beta$ with the property that for every $ t$ there is a $ \tau > t$, continuously varying with $ t$, such that
$\displaystyle \beta(t) + L\,\mathbf{T}_\beta(t) = \beta(\tau)- L\, \mathbf{T}_\beta(\tau).$
In fact, we only need to construct a finite segment of such a back-tire track as once it is created we can extend a sufficiently nice back tire track indefinitel, see Part II of the Solution, Extending the Track.

To briefly describe the construction of this initial back-tire track segment, we will suppose that we already have some ambiguous tracks and describe some of the necessary conditions on a segment of the back-tire track. The defining characteristic for a back-tire track of ambiguous tracks implies that we may suppose that the back-tire track $ \beta:[0,1] \to \mathbf{ R}^2$ is parameterized in such a manner that

$\displaystyle \beta(0) + L\,\mathbf{T}_\beta(0) = \beta(1) - L\, \mathbf{T}_\beta(1).$
This condition implies that the front-tire tracks
$ \alpha_f(t) = \beta(t) + L\,\mathbf{T}_\beta$ and $ \alpha_r(t) = \beta(t) - L\,\mathbf{T}_\beta(t)$
meet at $ \alpha_f(0) = \alpha_r(0)$, and thus places compatibility conditions on the geometry of an initial back-tire track segment at the end points of the segment, specifically the tangent vectors and the curvatures at the end points must be satisfy certain technical conditions (for the details consult Part I of the Solution Creating an Initial Piece of Track and The Geometry of Bicycle Tracks.)

We note that the construction of such an initial back-tire track and the technical conditions involved in describing the geometry of the tracks is the conceptually hard part of the process. However, once an initial back-tire track segment has been constructed, it is relatively easy to construct a front tire segment. The technical part of our construction method is extending the back-tire track, so we can continue extending the front-tire track. The extension of the back-tire track is accomplished physically by pushing the bicycle backwards steering the bicycle in such a manner as to keep the front tire on the newly created front-tire track, see the relevant animations at . The extension of the back tire in this manner is done mathematically by solving the differential equation that governs the physical construction. We can extend the front-tire track and the back-tire track in this manner to produce an arbitrarily long ambiguous tire track, at least give a sufficiently nice initial back-tire track.