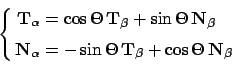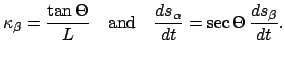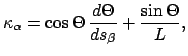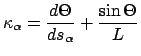Problem Statement I
Problem
Statement II
Solution to Original
Problem
Outline of Construction
of Ambiguous Tracks
Animations
and Examples
of Ambiguous Tracks
Geometry of Tire
Tracks
Part I of Solution:
Creating an Initial
Piece of Track
Part II of Solution
Extending the Track
References
|
Geometry of Bicycle Tracks: Page 3
From experience from riding a bicycle, one has direct control over
the speed of the back tire
 and the turning angle, the angle between the unit tangent of the front tire track and
the frame of the bicycle (or the tangent of the back tire track), which we denote by
and the turning angle, the angle between the unit tangent of the front tire track and
the frame of the bicycle (or the tangent of the back tire track), which we denote by
 .
For our purposes, the turning angle needs to be signed and satisfy the inequality .
For our purposes, the turning angle needs to be signed and satisfy the inequality
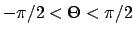 .
This sign requirement is so that we can distinguish between a right hand turn
and a left hand turn. We use positive angles to denote a left-hand turn and negative
angles to denote a right-hand turn. The restriction that the angles must be less than a
right angle implies that .
This sign requirement is so that we can distinguish between a right hand turn
and a left hand turn. We use positive angles to denote a left-hand turn and negative
angles to denote a right-hand turn. The restriction that the angles must be less than a
right angle implies that
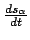
and

have the same sign, and will hold until a singularity develops in
the tire tracks.
We can now write the differential equations relating
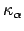
and

in terms of the these natural controls for a bicycle. This will allow
us to create a bicycle track in a natural fashion by specifying how
the bicycle is turned and how fast the bicycle is travelling. First, we note
that the angle
 relates the Frenet frames of the front tire and the back tire,
relates the Frenet frames of the front tire and the back tire,
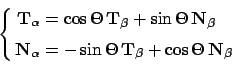 |
(1) |
This gives us
and thus
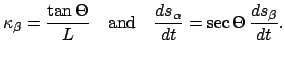 |
(2) |
We can now write differential equations as
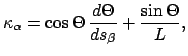 |
(3) |
where we interpret
 as
as
 .
We can rewrite (3) as .
We can rewrite (3) as
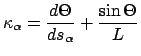 |
(4) |
These differential equations allow us to create a pair of tire tracks
knowing how the bicycle is turned and the speed of the back tire by
solving the relevant Frenet frame equations. In particular, these differential
equation allow us to construct the back-tire track knowing the front-tire
track, as knowing the curvature of the front-tire track we can solve
for the angle
 ,
which then determines the curvature of the back tire track. The tracks
can then be recovered by solving the relevant Frenet frame equations. ,
which then determines the curvature of the back tire track. The tracks
can then be recovered by solving the relevant Frenet frame equations.
|