Homework hints
Notes:
- Assignments and due dates are in the Schedule and Lessons sections.
- Unless otherwise noted all problems assigned from the text are from the "Problems: Developing Engineering Skills" sections.
- Also note that answers are not guaranteed to be correct. I can make a numerical goof as easily as you can. Work towards understanding, not towards a number.
| Problem | Hint | Answer | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1-1 [download] |
Be careful with your units! A helpful conversion is that a m2/s2 is the same as a J/kg, not a kJ/kg, which is the typical set of units for enthalpy. | 0.530 kg/s, 184.6°C, 38.7 cm2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1-2 [download] |
Again, careful with the units! You will most likely need to convert liters to m3. Thermo books can get a little sloppy with their language sometimes. It would be better to say "find the power per unit mass flow rate" than "find the work per unit mass". That is, Wdot/mdot instead of W/m. |
285 kJ/kg, 4.06 kW | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2-1 [download] |
You will need conservation of energy for a closed system over a finite time, the ideal gas equation, and relationships for Δu and Δs for an ideal gas with constant specific heats. But wait, there's more! pd A useful relation to remember: R = cp - cv. |
Qin,12= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2-2 [download] |
From entropy accounting you see that the terms "adiabatic" and "reversible" always imply "isentr..." | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3-1 [download] |
Does this look almost exactly the same as 2-1? Yes! Will the answers be about the same? Yes! But will the tools be different? Yes, yes, yes! You now must use the ideal gas tables for air to find u and so (not s–remember that so is only a piece of s). A useful relation to remember: R = cp - cv. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3-2 [download] |
See hints for 2-2 and 3-1. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5-1 [download] |
Remember to assume it's saturated first, and then compare your actual given properties to the saturation properties. | (a) Two-phase (saturated) mixture. (d) subcooled (compressed) liquid |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5-2 [download] |
This is all about interpolation (and in one case, double interpolation [which really means three times!]). If you want a primer on interpolation, check out the Youtube video solution for Example 1 in Lesson 2 in the Files section. (Interpolation help starts at 5:55.) | (b) 260° | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| M&S 3.30 | You already have experience finding property values. Here is more, 'cuz we want you to be perfect. (Well, perfecter. ☺) Equally as important here is learning to identify the states on P-v and T-v diagrams. We have seen in class that skething these before applying conservation equations can save you muchísimo tiempo. |
(b) u=2678.0 kJ/kg (c) This is a supercritcal fluid! (d) h=2371 kJ/kg |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| M&S 6.3 | See hint for 3.30. | (b)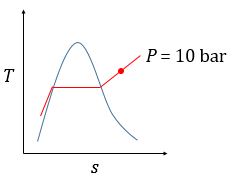 (c) 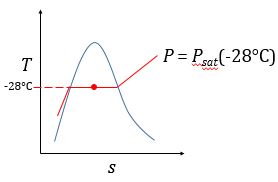
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| M&S 6.89 | What is the purpose of a compressor? Does power go in or out? What are you going to do with "adiabatic" and "reversible" given to you in the problem statement? Is this enough to fix the state of the stuff leaving the compressor (meaning you have two independent, intentive properties)? |
0.531 kg/s | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| M&S 3.35 | Can you use ∫Pd Note that the authors are asking you to find heat transfer in units of B/lbm, which is more appropriately called "heat transfer per unit mass." This is important because you do not know what the mass is, nor can you ever solve for it! An extra variable m will be floating around in your solutions, then. (One trick you can use is to set m=1 lbm, and then everything is by definition per unit mass.) |
486 B/lbm out | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| M&S 6.18 | Can you use ∫Pd Also see hints in 3.35 about the whole "per unit mass" deal. |
Q1→2/m = 110 B/lbm out | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| M&S 6.98 |
Since you are given an isentropic efficiency, you will need to write conservation of energy for a pretend compressor for which s2=s1 to find the pretend work/mass (power/mass flow rate) first. How does the real work/mass (power/mass flow rate) compare to that? Now that you know the real work/mass, how will you find the real exit temperature? |
131.1 kJ/kg in | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| M&S 6.94 | This is an ideal gas with constant specific heats and so you don't need any property tables here! Woo-hoo! Use a value of cp = 1.004 kJ/kg·K to get the answers here. You will need the relationships for Δh and Δs that you learned in ConAps and that we reviewed early in the quarter. If you are using a bunch of plug and chug formulas that make use of k then you most likely don't understand the concepts fully. We'll make use of k relations later in the quarter... You will need to assume a value of T0. 20°C is a typical choice. (Can I leave it as 20°C though?) |
(a) 837.2 K | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| M&S 7.11 | Basically pluggin' and chugign' into the formulas for exergy. Do note, however, the relative effects of elevation change versus temperature change on the exergy content of the water, which you just might screw up if you don't take into account your units correctly! Specifically, remember that m/s2≠kJ/kg, but rather m/s2=kJ/kg. | (b) 152 m | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Flow Exergy HW#1 [download] |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| M&S 6.35 | You will need the closed system, finite time vesion of the accounting of entropy. Note that the text uses the term "entropy production." This is synonomous with "entropy geration." | (a) Sgen = 0 (b) Sgen = 0.353 Btu/lbm·°R |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.23 | Don't forget the KE and PE components of the exergy. Also pay attention to your units when including KE and PE in exergy terms. Remember that you must evaluate the properties of the stuff at T0 and P0, not the properties of the environment itself when finding exergy. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.33 | Note which answers are the same and which are not. Exergy itself is just a property, but exergy destruction is process dependent. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13-1 [download] |
A throttling process is designed to greatly reduce pressure over a small distance in the direction of flow. Throttling valves have no moving parts, you don't plug them in, and the surface area is too small for there to be any heat tranfer. 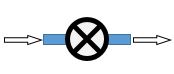 A throttling valve The rate of exergy coming in/going out is due to mass flow. Which term(s) in the Accounting of Exergy are those? As is often the case, you will have to assume a T0 and/or P0. Typical values are around STP. I assumed 20°C for the answer provided here. |
Ȧdes = 96 kW | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Flow Exergy HW#2 [download] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.68 | Since you do not have a mass gflow rate, you can oly calculate a heat transfer per unit massf low rate, q=Qdot/mdot. If you prefer, you can just make mdot=1kg/s, and by definition everything is now per unit mass flow rate. In the case of the waster heat, the exergy destruction is due to heat transfer through a finite temperature difference. In the resistive heating case, it is due to the Ohm's Law (electrical resistance is basically electric friction). Though you will find that the exergetic efficiency for the waste heat system is higher, that could change drastically as Tb increases. |
εwaste heat = 26.7% | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7.115 | As was true with the in class example and in the Flow Exergy HW Part 2, we are interested in the net flows if exergy with a given fluid stream. Also, "work per unit mass" is better interpreted, in my opinion, as "power per unit mass flow rate." | εoverall = 88.9% | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8.4 | Much like in class example. Remember that the inlet to the pump is saturated liquid and the inlet to the trubine is saturated vapor for the ideal cycle. (The exit of the turbine will be a mixture. How do you know? Draw the T-s diagram!) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8.23 | Since the properties have been given to you, you have a lot less work to do. Having said that, I want you to draw all the system components that make up the cycle, and obviously you will identify systems as separate drawings whenever you apply a ConAps principle! | 31.4% | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8.26 | In some sense this is straight forward—just go around the cycle and analyze one component at a time and apply property relations. In another sense it is hard, because sometimes you will have to go on to the next component before you have everything you need. Try not to let that bug you. Eventually you will have all you need. Speaking of which, note that the mass flow rates going through different parts of the cycle are different. For example, the high pressure turbine and the low pressure turbine have different flow rates. How might you deal with that? I would suggest assuming that the massflow rate through the first stage (high pressure) turbine is 1.0 kg/s. The mass flow rate going through the second stage (low pressure) is an unknown. When you eventually get to analyzing the open feedwater heater you will be able to get that number. Also keep in mind that when you are calculating the efficiency, these different mass flow rates will need to be accounted for. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9.35 | I highly recommend you work in symbols only, and then automate the number crunching using the ideal gas property calculator. Just plug in the new values of P2 and run with it. Remember, however, that the electronic property calculator is not the same set of tables as in your text. Namely, there is no s0 function in the electronic version. However, you shouldn't need it, should you? The back work ratio is nothing more than the ratio of pump power in to power out (not net power out). Note that these are larger for gas vapor cycles than for vapor power cycles. Why is that? |
P2/P1=6: η=37.7% P2/P1=8: bwr=0.372 P2/P1=12: Wdot,net=2535 kW |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9.44 | The regenerator effectiveness is the same idea as a heat exchanger effectiveness (which is what the regenerator is in this case) that you will study or have studied in your Heat Transfer Class. It is the ratio of the actual rate of heat transfer delivered to the cooler stream (as seen by the increase of h for realz) divided by what you would get if the heat exchanger were infinitely long. In the infinitely long case, the cooler stream would heat up all the way until it has the same T as the entering hot stream. |
mdot= 43.2 kg/s Qdot,in=30.2 MW |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9.3 |
Remember, each step in the cycle is made up of a finite time, closed system process. Apply CoE and property relations to each step, and go on to the next one. |
(a) 0.672 kJ (c) 50.6% |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9.13 | This is a cold air standard cycle! "But it just says 'air standard,' you say. Yes! But notice how you are also given a constant value of cv? Hence, cold air standard... As in 9.3, each step in the cycle is made up of a finite time, closed system process. Apply CoE and property relations to each step, and go on to the next one. It is also useful to remember that for an ideal gas, R = cp - cv. You can find W2→3 with CoE, or you can use W2→3 = m∫23Pdv where pvk = constant. You should be able to tell me why! Lastly, note that from 3 to 1, there is both Q and W. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10.17 | Round and round the cycle you go... |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12.1 | Just a simple mass basis to mole basis analysis problem. Set up a table like the in-class examples, but remember that in those examples we were going from mole to mass. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| LE25_HW [Download] |
I highly recommend you pick a closed system consisting of both gases before and then afer the valve in opened. ("Before" and "after"? Hmmm... Wonder what form of CoE I should use?) You could try pd In reality, the only new part of this problem compared to others in the past is that you have more work to do in finding your properties, since it is a mixture of ideal gases. Treat the mixture as an ideal gas with variable specific heats. And yes! you can use your magic electronic property tables, but use the program for ideal gases, and use it on a molar basis. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12.12 | As long as the composition isn't changing (and it's not) any specific property can be found with What would this be on a molar basis? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12.24 | You'll need incroporate the the mixture composition into conservation of energy as well. Try to massage your conservation of energy equation to the point that you have separate expressions for the specific enthalpy change for both Ar and CO2. Also note that you will NOT use property tables here, but rather assume constant specific heats to find the changes in h. In part (c) don't forget that Dalton's Model requires partial pressures for specific entropy changes! |
(b) 431 K (c) 0.240 kW/K |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12.30 | Keep in mind that φ=Pv/Pg. What temperature will you use for Pv? For Pg? Why? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12.34 | If no condensation occurs, then ω2=ω1. If condensation does occur, that what does ω1 - ω2 give you? Also helpful here is ω = 0.622[Pv/(P-Pv)] = 0.622[Pv/(P-φPg)], where P is the plain old pressure (total pressure, mixture pressure, barmoetric pressure, whatever you wanna' call it.) This works for ω1 and ω2. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29-1 [Download] |
The problem asks you to use the equations, but that doesn't stop you from checking your answers via the pysch chart. | (b) Pv=0.177 psi, φ= 0.412 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12.48 | Now there is a really hard way to do this, which involves using the equations to find your properties instead of the pysch chart. (I.e., hmix=ha(T)+ωhg(T) and hw=hf and so on.) That will give you an analytic solution to solve for ω explicitly. (And if you cheat and use the solutions manual, that is what you will do and probably not understand any of it.) But there is another way that is much easier and that does let you use the pysch chart. What is it? Alrighty, then. Try this. Do conservation of mass for the water only and then substitute that result into conservation of energy. You will get a term in CoE that looks like this: (ω2-ω1)hf. What are typical values of ω? How big would (ω2-ω1) be, then? And finally, how big is (ω2-ω1)hf compared to hmix1 and hmix,2? That's right! Virtually negligible! Give that a shot... |
φout=0.296 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12.52 | ṁw=0.639 lbm/min | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12.50 | Almost exactly the same as in-class example, but with different numbers |
Q̇ = 804.1 kJ/min | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12.59 | If you did not use the pysch chart, you would have to iterate! Also note that this is a case where the conservation of mass on dry air only is imporant. The rates of dry air at (1), (2), and (3) are all different! |
φ = 40% | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13.9 | You absolutely must—no two ways about it, can't even for a second consider not—balance the theoretical reaction first. Percent excess, percent theoretical, etc. are referenced to the theoretical reaction, and cannot be taken into account in a balanced reaction final reaction in one step. |
ṅair = 1.182 kmol/h | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13.13 | You will have to go back to psychrometric basics to do part (b)—you cannot use the pysch chart. (You should be able to tell me why.) |
(b)44.8°C |
⇧