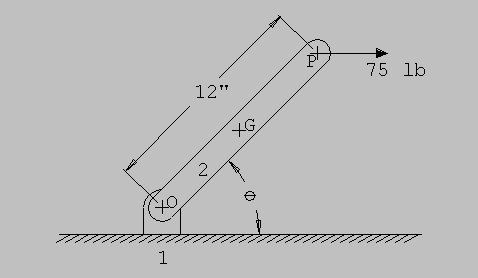
Design Problem #1

Winter 1997-98

. The 10 lb link shown is 12 inches long, has a constant horizontal force of 75 lb applied at P and is driven by a motor at O. At time, t=0, the angle theta_o = 45, angular velocity omega_o= 20 rad/s, and the constant angular acceleration, alpha = 10 rad/sec² As the link moves through one rotation, the angular velocity increases. Counter-clockwise rotation is positive.

The best link for the job is one which will produce the smallest reaction force and require the lowest torque (T12) to produce the given velocity and angular acceleration. Parameters which you can easily vary are the radius of gyration, the mass and the location of the center of mass. (These values determine the mass moment of inertia). Use the following constraints: 0.05 ft < k_g < 0.5 ft 0.05 ft < r_og < 0.5 ft

However, there are usually trade-offs in design. If you move the mass center of the link closer to point O, you will need additional mass to stiffen the link between the CG and point P. Assume the following (somewhat arbitrary) relationship. If the CG of the link is halfway between P and O, the weight of the link is 10 pounds. For each inch, x, that you move the CG away from the center of the link, the weight increases by 2|x|³ pounds (where x is in inches). For example, if you place the CG of the link 4 inches from point O the weight will be 10 + 2(6-4)³ = 10 + 16 = 26 pounds.

The figure-of-merit (FM) for your design can be determined using the torque multiplied by the reaction force, FM = |T₁₂*F₁₂|. Since T12 and F12 vary with angle , you will need to calculate the FM in 5 degree increments from 45 to 405 degrees. The figure-of-merit for your design will be the largest FM value calculated. If FM for your design is the lowest of all designs that meet the specifications, then you will have the best design. (We determine FM by maximizing with respect to , but the design should minimize that maximum).

Numbers to compare:

For a 12 pound link with the CG 5 inches from point O and radius of gyration = 3.5 inches at time, t=0.293 s = 7.07 rad
(This analysis includes weight)

F₁₂ = 141 lb

T₁₂ = 57.8 ft-lb

FM = 8.15 x 10³ ft-lb^2

Return to top of page

Link to ME304 syllabus

Link to ME304 information

Questions or comments? Contact Dr. Lee Waite

This file was last updated on December 9, 1997

: