Wideband FM can be Tricky
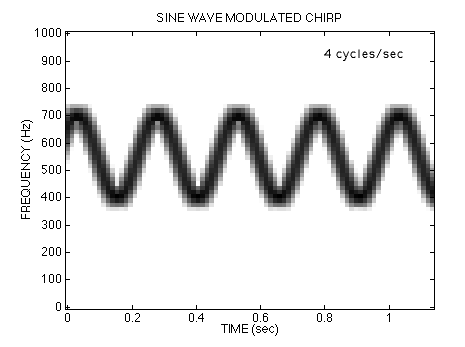
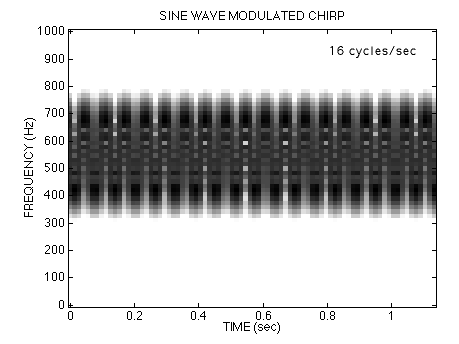
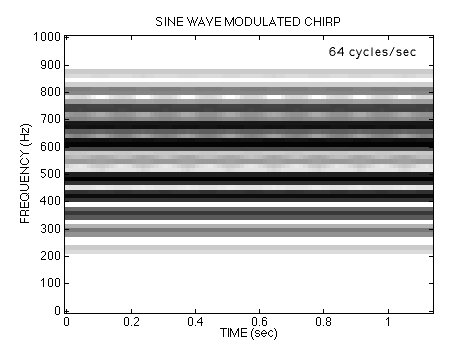
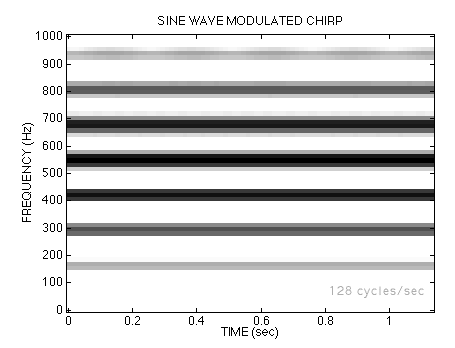
Listen to each of the signals again by clicking on the waveform. Keep in mind that only the chirp rate is changing. In all cases, the fi(t) formula predicts that the instantaneous frequency would oscillate between 400 Hz and 700 Hz.
Click on the names below to display a larger version of the
spectrograms.
4-Hz Sine-wave modulated FM ,
16-Hz Sine-wave modulated FM ,
64-Hz Sine-wave modulated FM ,
128-Hz Sine-wave modulated FM .
Doesn't the 64 cycle case sound like a vowel--maybe "aaah" or "owe"?
Notice that the previous ideas about the frequency content of the FM signal are no longer valid !
If the modulation rate gets too large, then our perception of the sounds changes. However, the change is not necessarily a loss, since the chirps created with high-frequency sine waves in their argument seem to posses a harmonic quality (i.e., the spectrum exhibits a number of isolated spectral lines). This fact is the basis of FM synthesis for various musical instruments.
Carson's rule gives the bandwidth of an FM signal as
an approximation that sort of works for both narrow
band and wideband cases.
Let fm be the highest frequency in the **modulating**
signal. Let Df be the maximum frequency deviation,
which is related to the amplitude of the modulating
signal. Let fc be the carrier frequency. Then the
bandwidth (BW) of the FM signal (centered on fc) is
Thus for narrow band FM, DF--> 0 and BW =2fm. For wideband FM, Df >> fm and BW = 2Df. Sometimes you see the formula given in terms of "beta", where beta=Df/fm.
Beta can also be related to a parameter of Bessel functions that arise when you use as the signal model
If you differentiate the instantaneous frequency of this signal you get
so beta fm = Df, the maximum frequency deviation about the carrier.
MATLAB
These were generated with MATLAB. Click here to see the code that computes and displays the spectrograms.
Go back up to continue.