| Table of Contents |
Crummett and Western, Physics: Models and Applications,
Sections 9-4,5
Halliday, Resnick, and Walker, Fundamentals of Physics (5th
ed.), Sec. 10-1 to 10-3
Tipler, Physics for Scientists and Engineers (3rd ed.), Sec.
7-3,6
The theorem of conservation of linear momentum states that, if the vector sum of the external forces on a system of particles is zero, then the total linear momentum of the system remains constant, no matter what parts of the system may do. For a system of just two objects moving in one dimension, on which no net external force acts, this gives

![]() (1)
(1)
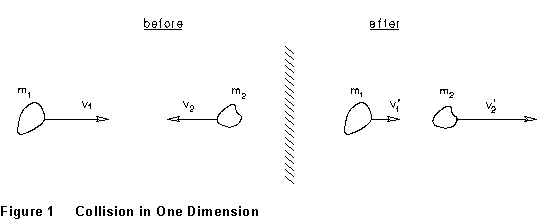
where m1 and m2 are the masses of the two particles, v1 and v2 their respective velocities at some instant, and v1' and v2' the velocities at some other instant. (In Eq.(1), all v's are positive to the right -- in Figure 1, v2 would have a negative value.) In the case of a collision, v1 and v1' might be the velocities of object #1 just before and just after the collision, etc. Momentum conservation is particularly useful in collision-type situations, in which, typically, by far the most important forces are the internal forces that the two colliding objects exert on one another during the collision. Collision forces can frequently be assumed to be so strong that, just during the collision, other forces, even if not zero, can be ignored just during the collision.
In an isolated system, momentum is conserved regardless of the nature of the forces of interaction. If these forces are conservative, mechanical energy as well as momentum will be conserved in the collision. Such an event is called a perfectly elastic collision. In a perfectly elastic collision, the relative speed of the two objects is the same before and after the collision:
![]() (2)
(2)
Real collisions are not perfectly elastic. The "degree of elasticity"
of a collision is often expressed in terms of a quantity called the coefficient
of restitution ![]() of
the collision.
of
the collision. ![]() is
defined as the ratio of the final to the initial relative speed of the
two colliding bodies:
is
defined as the ratio of the final to the initial relative speed of the
two colliding bodies:
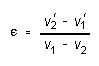 (3)
(3)
![]() can never be greater than
1, and would be exactly 1 for a perfectly elastic collision.
can never be greater than
1, and would be exactly 1 for a perfectly elastic collision.
The opposite extreme would be a perfectly inelastic collision,
in which all the relative motion disappears: the two objects
stick together and move as one object after the collision.
For a perfectly inelastic collision, plainly, ![]() =
0.
=
0.
In this experiment, you'll measure the velocities of two gliders moving on a horizontal air track, before and after they collide. By comparing the total momentum before and after the collision, you can determine how closely Equation (1) applies in this situation.
Before you carry out this experiment, you should have gone through the preliminary exercise on position and velocity measurements using the Sonic Ranger, which appears at the beginning of this chapter. If you have not done so, you should go through that exercise now, before you proceed with this experiment.
(1) Start the computer software and carry out the temperature calibration as directed.
 (2) Turn
on the air-track blower (air setting 3). Start the data collection as usual.
Verify that the Ranger can "see" both carts over the central
region of the track. When properly aligned, the sonic ranger will trace
both moving carts at once (it records successive echoes alternately in
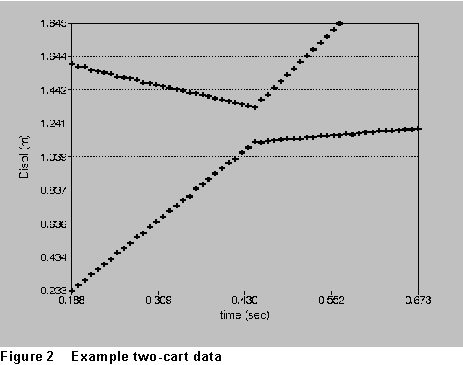
one data set, then the other). For example, the collision sketched in Figure
1 (above) might produce data like that shown in Figure 2.
(2) Turn
on the air-track blower (air setting 3). Start the data collection as usual.
Verify that the Ranger can "see" both carts over the central
region of the track. When properly aligned, the sonic ranger will trace
both moving carts at once (it records successive echoes alternately in
one data set, then the other). For example, the collision sketched in Figure
1 (above) might produce data like that shown in Figure 2.
(3) Some alignment of the sonic ranger transducer will most likely be needed. If you cannot get two satisfactory data traces, call the lab instructor for help with alignment.
(4) Your object in this laboratory is to examine the conservation of momentum for the collision of two air-track gliders. The Sonic Ranger will acquire position vs. time data during the collision. You will collect data on at least three different collisions. One collision must be (nearly) elastic, the spring ends of the two gliders colliding; one collision must be completely inelastic, the two colliding gliders sticking together; the third is up to you, but do not simply repeat one of the others. Vary the mass of at least one cart.
(5) GENTLY push the gliders toward one another and allow and capture the record of their collision with the Sonic Ranger. Save the data to a file.
(6) Repeat this procedure for at least two other collisions. Describe each one, and how you set it up and carried it out, in your lab notebook. Of the three collisions, one must be (nearly) elastic and one must be (perfectly) inelastic.
(1) For each of your runs, perform line fits on the position-vs-time data to find the slope of each x-t graph (the velocity of each glider before and after the collision -- that is, four line fits per collision experiment.)
(2) In your final report show (1) The slope of each straight line, and (2) graphs of the data used for all three collisions (show the best-fit lines on at least one of the graphs for each of the three).
(3) Calculate the total momentum of both gliders before the collision and after the collision with uncertainties propagated from the uncertainties in v given by the fitting procedure, and the uncertainty in the masses. Compare the total momentum before to the total momentum after for each collision. Calculate the percentage difference in the before and after values. Tell whether your values agree with the conservation of momentum to within the experimental uncertainty.
(4) If the total momentum calculated in (3) above is small (as compared to the momentum of a single cart for example) it may appear that there is a large percentage change in the total momentum of the two-cart system as a result of the collision. You may be inclined to conclude that momentum is not conserved.
In head-on collisions, the total momentum (p1 + p2)
is fairly small. In this case it is more revealing to compute ![]() =
pf - pi for each cart. Compart the numerical
value of
=
pf - pi for each cart. Compart the numerical
value of ![]() for one cart
to the value of
for one cart
to the value of ![]() for
the other cart. (Use uncertainty in velocity from fitting and uncertainty
in cart mass to find the uncertainty in each
for
the other cart. (Use uncertainty in velocity from fitting and uncertainty
in cart mass to find the uncertainty in each ![]() )
)
Do the ![]() values have
the same sign? Make an argument based on Newton's laws for the
values have
the same sign? Make an argument based on Newton's laws for the ![]() values
to have opposite signs.
values
to have opposite signs.
Report whether the magnitude of ![]() for
one cart equals the magnitude of
for
one cart equals the magnitude of ![]() for
the other within estimated uncertainties.
for
the other within estimated uncertainties.
(5) Calculate the coefficient of restitution for each collision.
Moments of Inertia: The Physical Pendulum
last update 7/98