Chapter 3: Mechanics Experiments
Moments of Inertia: The Physical Pendulum
References
Crummett and Western, Physics: Models and Applications,
Sec.11-2,3,4 and 14-2
Halliday, Resnick, and Walker, Fundamentals of Physics (5th
ed.), Sec. 11-6,7,8, Sec.16-6
Tipler, Physics for Scientists and Engineers (3rd ed.), Sec.
8-2
Introduction
 The mass of
an object is a measure of its inertia -- that is, its resistance
to a change in its state of motion. In the rotational motion of a rigid
body, the quantity that plays the analogous role depends not only on the
body's mass, but also on how the mass is distributed in space relative
to the axis of rotation. This quantity is the rotational inertia, or moment
of inertia, I. The rotational inertia in turn is often expressed
as
The mass of
an object is a measure of its inertia -- that is, its resistance
to a change in its state of motion. In the rotational motion of a rigid
body, the quantity that plays the analogous role depends not only on the
body's mass, but also on how the mass is distributed in space relative
to the axis of rotation. This quantity is the rotational inertia, or moment
of inertia, I. The rotational inertia in turn is often expressed
as
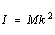 (1)
(1)
which defines the radius of gyration, k, about a particular axis
of the rigid body. k is a characteristic length which depends on
both the size and shape of the body, and M is its mass. The radius
of gyration of a uniform disc of radius R about its axis, for example,
is 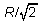 ; this is just
another way of saying that the rotational inertia of a disc is given by
½MR2.
; this is just
another way of saying that the rotational inertia of a disc is given by
½MR2.
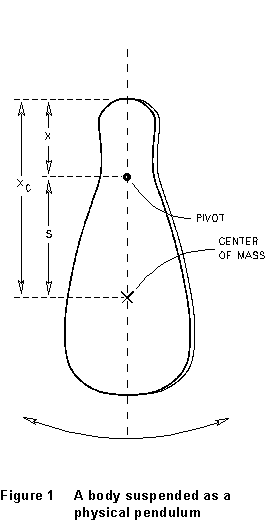
A physical pendulum consists of any rigid body pivoted about a horizontal
axis and free to swing back and forth in the vertical plane, as sketched
in Fig. 1. The distance from the pivot to the body's center of mass is
s, and the mass of the body is M. The period of the physical
pendulum's oscillation is given by
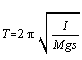 (2)
(2)
You'll find a derivation of this in your textbook. In (2), I
is the moment of inertia about the pivot point. But using the parallel-axis
theorem, we can write this as
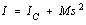
where
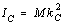 (3)
(3)
is the moment of inertia about a parallel axis through the center of
mass of the body and kC is the radius of gyration for
the axis which passes through the center of mass. Finally, substituting
(3) into (2) gives
 (4)
(4)
In the present experiment, you will infer kC and s
from measurements of the period of the physical pendulum swinging about
different pivot points; from these, you can infer both its rotational inertia
about the center of mass and the location of the center of mass.
It is obvious from (4) that the period T becomes very long for
large s, and also as s goes to 0; thus there must be an intermediate
value of s for which T is a minimum. It is easy to
show that this occurs when s = kC, so that
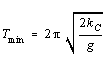 (5)
(5)
Thus, by finding the minimum period of oscillation, you can determine
kC directly.
Equipment
- Physical pendulum with adjustable pivot
- Meter stick
- Timer
Procedure
Your physical pendulum is a large flat piece of wood or plastic which
can be pivoted at various points along its midline, as suggested
by Fig. 1.
(1) Sketch the object to scale in your laboratory notebook, and
record all its dimensions.
(2) Pivot the pendulum near its end and set it swinging. The
amplitude of the swing shouldn't be very large, no more than 15-20 degrees.
Measure the time it takes for the pendulum to undergo 10 complete cycles
of its oscillation. Trade jobs with your partner, and repeat the measurement.
Now each partner take another time measurement, so that you have four independent
trials of the time required for the pendulum to swing through 10 cycles.
(3) Measure the distance from the end of the object to the pivot
point (distance X in Figure 1).
(4) Repeat steps (2) and (3) for several other pivot positions
along the midline of the body (something like 7-12 different positions
should be enough). Your primary purpose is to determine the minimum
oscillation period; try to take data that will let you do so as precisely
as possible.
Analysis
(1) Derive Equation (5) from Equation (4).
(2) For each pivot position, calculate the mean value and standard
error of the pendulum's period. Draw a graph of T vs. X, and from
it determine the minimum value of the period, Tmin.
(You may want to use an expanded scale, or plot transformed values, or
something, to make the minimum more sharp and clear.) Use Equation (5)
to calculate the corresponding value of the radius of gyration kC.
From the errors in your T-values and in your graph, estimate the
uncertainty of Tmin and the corresponding uncertainty
in kC. (See Chapter 2 if you need to review error-propagation
calculations.)
(3) Compare your final value of kC with the
scale drawing of your physical pendulum. Remember that kC
is the effective distance (for rotational motion) of the body's mass from
its center of mass. Does the value you got appear reasonable? Comment.
(4) Choose several values of X and T for which
T is substantially different from Tmin.
For each, use Equation (4) and your experimental value of ks
to calculate s. Make a table of X, T, s, and
XC = X + s. (See Fig. 1.) XC
is the position of the center of mass of the object. Calculate the mean,
standard deviation, and standard error of the values of XC
that you get. Indicate the position of the center of mass on your scale
drawing of your pendulum.
(5) You can also locate the center of mass by determining the
pivot position at which T = Tmin. From the discussion
around Equation (5) we can see that, if the period has its minimum value
when X = Xmin, then XC = Xmin
+ kC. Determine XC, and estimate its
uncertainty, by this method. Which means of determining Xmin
do you think is preferable? Why?
Angular Acceleration and Moment of
Inertia
last update 6/97
 The mass of
an object is a measure of its inertia -- that is, its resistance
to a change in its state of motion. In the rotational motion of a rigid
body, the quantity that plays the analogous role depends not only on the
body's mass, but also on how the mass is distributed in space relative
to the axis of rotation. This quantity is the rotational inertia, or moment
of inertia, I. The rotational inertia in turn is often expressed
as
The mass of
an object is a measure of its inertia -- that is, its resistance
to a change in its state of motion. In the rotational motion of a rigid
body, the quantity that plays the analogous role depends not only on the
body's mass, but also on how the mass is distributed in space relative
to the axis of rotation. This quantity is the rotational inertia, or moment
of inertia, I. The rotational inertia in turn is often expressed
as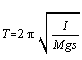 (2)
(2)  (4)
(4) 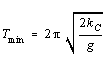 (5)
(5)