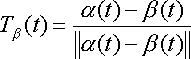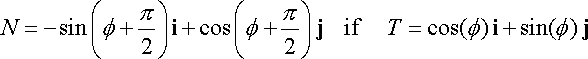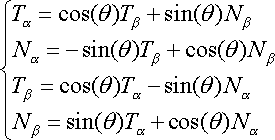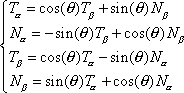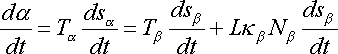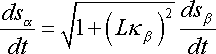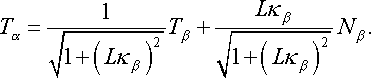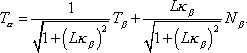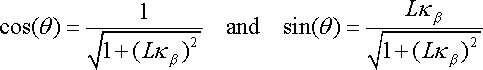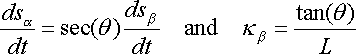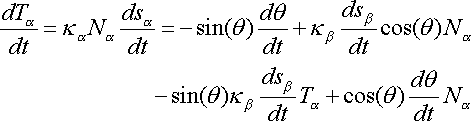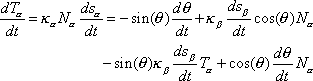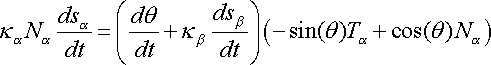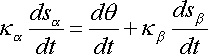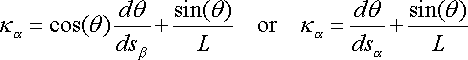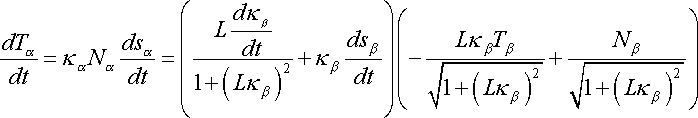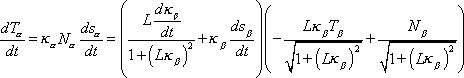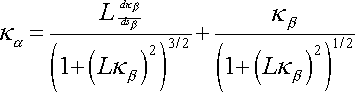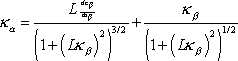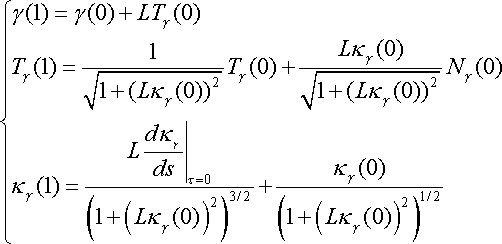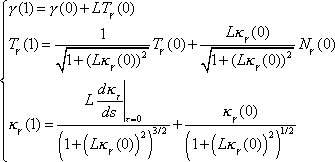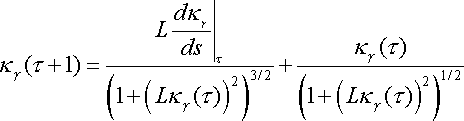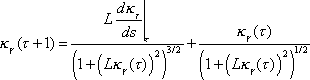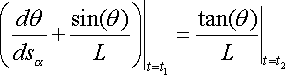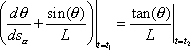Derivations of Equations
Recall that the question that we are studying is:
Do there exist any curves 
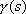

 parameterized with respect to arclength such
that the positions of the front tire and back tire of a bicycle at time
parameterized with respect to arclength such
that the positions of the front tire and back tire of a bicycle at time 


 ,
respectively satisfy
,
respectively satisfy 
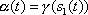

 and
and 
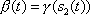

 for some positions
for some positions 
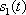

 and
and 
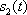

 of the curve
of the curve 
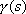

 ?
?
We will assume that the bicycle is ridden on a flat surface,
and that the bicycle is not banked into the ground, that is the plane of each
tire meet the ground in a right angle. We suspect that one can create a
unicycle track without these assumptions, but the equations become much more
complicated. In particular, using these
we have that
where L is the length of the bicycle and 
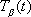

 is the unit tangent vector to the back tire
is the unit tangent vector to the back tire 
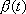

 at time t. Equation (1) arises from two simple observations concerning the
manner in which a bicycle is built. The
first observation is that the back tire is fixed in the frame, meaning that the
back tire and the frame are aligned.
This means that the tangent line to the back tire track at time t
is equal to the secant line through the front and back tire positions at time t,
that is
at time t. Equation (1) arises from two simple observations concerning the
manner in which a bicycle is built. The
first observation is that the back tire is fixed in the frame, meaning that the
back tire and the frame are aligned.
This means that the tangent line to the back tire track at time t
is equal to the secant line through the front and back tire positions at time t,
that is
The second observation is that the frame is rigid, meaning
that the distance between 
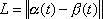

 the points of contact between the tires and
the ground is a constant independent if
the position of the tires.
the points of contact between the tires and
the ground is a constant independent if
the position of the tires.
Rather than express all the equations for describing the
tracks of a bicycle in terms of the tracks 
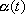

 and
and 
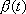

 ,
we describe the motion of the bicycle in terms of the angle
,
we describe the motion of the bicycle in terms of the angle 
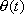

 between the unit tangent vectors of the
tracks, the angle between the planes of the tires. We use this angle because when riding a bicycle, we have direct
control of this angle since by controlling the angle
between the unit tangent vectors of the
tracks, the angle between the planes of the tires. We use this angle because when riding a bicycle, we have direct
control of this angle since by controlling the angle 
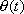

 and the speed of the bicycle the position of
the bicycle. We require the angle
and the speed of the bicycle the position of
the bicycle. We require the angle 
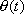

 be signed and satisfy
be signed and satisfy 
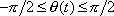

 to distinguish between a right hand turn and
a left hand turn. A left-hand turn will
have a positive sign and right-hand turn will have a negative sign, see diagram
below. This convention allows us to
quantify left and right by using the principal unit normal vector N(t)
for the curve, which is given by
to distinguish between a right hand turn and
a left hand turn. A left-hand turn will
have a positive sign and right-hand turn will have a negative sign, see diagram
below. This convention allows us to
quantify left and right by using the principal unit normal vector N(t)
for the curve, which is given by
If 
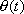

 is positive then
is positive then 
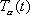

 lies on the same side of
lies on the same side of 
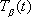

 as
as 
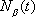

 ,
while if
,
while if 
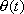

 is negative then
is negative then 
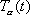

 lies on the same side of
lies on the same side of 
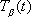

 as
as 
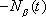

 ,
which from standard convention respectively corresponds to a left hand and a
right hand turn.
,
which from standard convention respectively corresponds to a left hand and a
right hand turn.
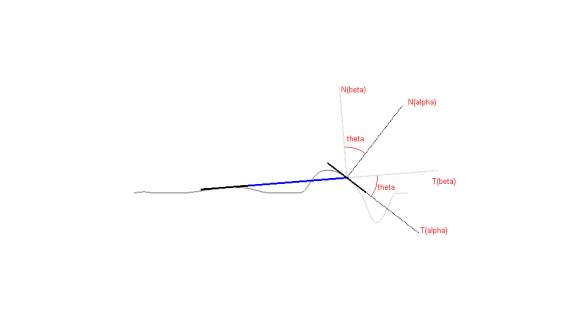
A principal use of the angle 
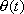

 is to convert between the two sets of
orthogonal basis vectors
is to convert between the two sets of
orthogonal basis vectors 
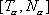

 and
and 
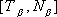

 . Using trigonometry and basic vector
arithmetic, we have
. Using trigonometry and basic vector
arithmetic, we have
By differentiating equations (1) to (3) with respect to
time, and using the Frenet frame equations, we derive the main equations needed
to construct a unicycle track with a bicycle.
Differentiating equation (1) respect to time, we get
where 
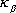

 is the signed curvature of the back tire
track, and
is the signed curvature of the back tire
track, and 
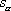

 and
and 
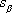

 are the arclength parameters of the curves
are the arclength parameters of the curves 


 and
and 
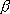

 respectively. There are a couple of important conclusions that we can make from
equation (4). Namely, that
respectively. There are a couple of important conclusions that we can make from
equation (4). Namely, that
and therefore
Equating the expression for 
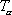

 in (3) and (6), we find that
in (3) and (6), we find that
from which we get
Differentiating the equation for 
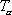

 in (3) with respect to t, we have
in (3) with respect to t, we have
which yields
Using that 
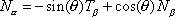

 ,
we have
,
we have
and thus implies that
The equations (8), (10), (11) allow us to construct a
bicycle track knowing the angle 
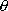

 as a function either arclength parameter
as a function either arclength parameter 
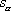

 or
or 
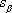

 since with this information we can solve the
Frenet frame equations to construct either the back tire track or the front
tire track. We could also solve the
Frenet frame equations knowing the angle
since with this information we can solve the
Frenet frame equations to construct either the back tire track or the front
tire track. We could also solve the
Frenet frame equations knowing the angle 
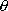

 and the speed
and the speed 
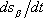

 of the back tire, which are of course the
physical controls of a bicycle.
of the back tire, which are of course the
physical controls of a bicycle.
It is also useful to have the curvature of the front tire in
terms of the curvature for the pact tire.
Differentiating (6) we have
thus
Equations (1), (6), (12) are useful for determining the
conditions needed on a bicycle track for it to be possible to create a unicycle
track with a bicycle. We need every
point on the front tire track to be a point on the back tire track. The equations (1), (6), (12) provide useful
relations between two points on the unicycle track, say 
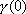

 and
and 
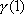

 ,
that correspond to
,
that correspond to 
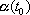

 and
and 
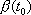

 . These equations say that for a unicycle
track to be created by a bicycle we need
. These equations say that for a unicycle
track to be created by a bicycle we need
where s is the arclength parameter on 
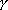

 and
and 


 is the parameter for
is the parameter for 
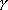

 . Repeatedly differentiating (12) with respect
to time or arclength we get conditions specifying the derivatives of the
curvature of
. Repeatedly differentiating (12) with respect
to time or arclength we get conditions specifying the derivatives of the
curvature of 
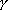

 when
when 
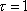

 in terms of the curvature and the derivatives
of the curvature when
in terms of the curvature and the derivatives
of the curvature when 
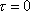

 . A cursory examination of these conditions
reveals that they are satisfied by having the curvature and the derivatives of
the curvature identically equal to zero when
. A cursory examination of these conditions
reveals that they are satisfied by having the curvature and the derivatives of
the curvature identically equal to zero when 
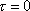

 and
and 
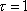

 .
.
To create a unicycle track with a bicycle, we first create a
track segment 
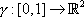

 with
with 
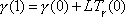

 ,
,

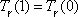

 ,
and the curvature and the derivatives of the curvature identically equal to
zero when
,
and the curvature and the derivatives of the curvature identically equal to
zero when 
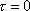

 and
and 
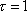

 .
Pushing the bicycle forward on the initial track segment, we can extend the
segment to the interval
.
Pushing the bicycle forward on the initial track segment, we can extend the
segment to the interval 
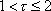

 by using the formula
by using the formula
The conditions on the curvature imply that the curvature and
the derivatives of the curvature when 
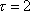

 are identically equal to zero, and therefore
we can extend the unicycle track forward indefinitely. We can also push the bicycle backwards on
the initial unicycle track to extend the track for
are identically equal to zero, and therefore
we can extend the unicycle track forward indefinitely. We can also push the bicycle backwards on
the initial unicycle track to extend the track for 
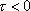

 . However, we can only guarantee that the
bicycle can be pushed for a short amount of time and arclength in the backwards
direction at present time, because we generate the backward direction for the
unicycle track by solving a differential difference equation. The differential
difference equation comes from noticing that for a unicycle track that can be
created with a bicycle there exists for every time
. However, we can only guarantee that the
bicycle can be pushed for a short amount of time and arclength in the backwards
direction at present time, because we generate the backward direction for the
unicycle track by solving a differential difference equation. The differential
difference equation comes from noticing that for a unicycle track that can be
created with a bicycle there exists for every time 
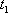

 a time
a time 
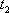

 with
with 
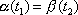

 ,
and therefore at every point we have two methods for calculating the
curvature. Thus by equating the
curvature of the back tire track at time
,
and therefore at every point we have two methods for calculating the
curvature. Thus by equating the
curvature of the back tire track at time 
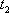

 to the curvature of the front tire track at
time
to the curvature of the front tire track at
time 
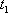

 ,
we have that the curvature of the unicycle track must satisfy
,
we have that the curvature of the unicycle track must satisfy
In terms of the angle 
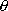

 which controls the construction of the
bicycle, this is equivalent to the equation
which controls the construction of the
bicycle, this is equivalent to the equation
Given an initial segment, 
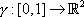

 ,
we can solve these differential difference equations for
,
we can solve these differential difference equations for 
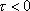

 only.
If we attempt to solve for
only.
If we attempt to solve for 
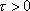

 we would overwrite the initial segment and
the extension of the initial segment by
we would overwrite the initial segment and
the extension of the initial segment by 
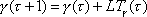

 .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()