Examples

ece200 | doering | ece labs | ece | rhit

Please note:

Install the TSCC codec in order to view the "Professor Solution" video clips.
Select the "28k" link if you are off campus using a modem, otherwise select the "128k" for better audio quality.
You need a soundcard in order to hear the audio discussion.
Click on the circuit thumbnail image to see the full size version.
Click and drag cursor over the "Answers" cell to reveal the answer, or click the answer icon . For best results, work the problem yourself, then reveal the answer.
Recently added examples are indicated by the icon.

Equivalent resistance

Circuit	Schematic	Problem Statement	*Professor Solution*	Answer
equiv 1		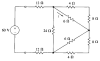Find the equivalent resistance seen by the 60-volt source.	28k / 128k	30 ohms
equiv 2		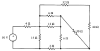Find the equivalent resistance seen by the 50-volt source.	28k / 128k	10 ohms

Node voltage analysis

Circuit	Schematic	Problem Statement	*Professor Solution*	Answer
nodal 1		Find the currents i₁ and i₂ using the node voltage method.	28k / 128k	2A, 4A
nodal 2		Find the current i using the node voltage method.	28k / 128k	1.5A
nodal 3		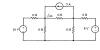Find the current i using the node voltage method.	28k / 128k	4 A
nodal 4		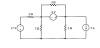Find the power delivered by the 17-volt source and the 2-amp source using the node voltage method.	28k / 128k	51 W, 4 W
nodal 5		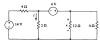Find the current i and the voltage v using the node voltage method.	28k / 128k	1 A, 6 V
nodal 6		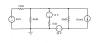Find all node voltages using nodal analysis.	28k / 128k	30 V, -8 V, 7 V, -20 V
nodal 7		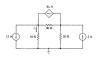Find all node voltages using nodal analysis.	28k / 128k	40 V, -280 V
nodal 8		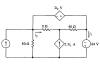Find the currents i₁ and i₂ using the node voltage method.	28k / 128k	8 A, -4 A
nodal 9		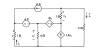Find I and V using nodal analysis.	28k / 128k	-2 A, -8 V
nodal 10		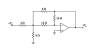Find the gain of the circuit using nodal analysis.	28k / 128k	-0.5

Superposition

Circuit	Schematic	Problem Statement	*Professor Solution*	Answer
super 1		Find the voltage V.	28k / 128k	6.67 volts
super 2		Find the voltage V.	28k / 128k	8 volts
super 3		Find the voltage V when R is 2 ohms	28k / 128k	8 volts
super 4		Find i using superposition. Hint: Find the currents i₁ and i₂ first.	28k / 128k	3 amps

Proportionality

Circuit	Schematic	Problem Statement	*Professor Solution*	Answer
prop 1		Find the voltage V_o.	28k / 128k	3.75 volts
prop 2		Find the current i using the proportionality method.	28k / 128k	714 mA
prop 3		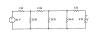Find the voltage v using the proportionality method.	28k / 128k	8 V
prop 4		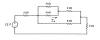Find the current I using the proportionality method.	28k / 128k	313 uA

Source transformations

Circuit	Schematic	Problem Statement	*Professor Solution*	Answer
source 1		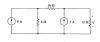Find the voltage V using repeated source transformations.	28k / 128k	48 volts
source 2		Find the power associated with the 6-mA source using repeated source transformations.	28k / 128k	-12 mW
source 3		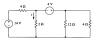Find i using source transformations.	28k / 128k	1 A

Thevenin / Norton equivalents

Circuit	Schematic	Problem Statement	*Professor Solution*	Answer
thev 1		Find the Thevenin equivalent circuit as seen to the left of terminals a-b, then find the current i.	28k / 128k	28 V, 8 ohms 2 amps
thev 2		Find the Thevenin equivalent circuit as seen by the 4-ohm resistor, then find v.	28k / 128k	6 V, 8 ohms 2 V
thev 3		Find the Norton equivalent as seen by the 4-ohm resistor, then find i.	28k / 128k	17.5 V, 10 ohm 1.25 A

Mutual inductance

Circuit	Schematic	Problem Statement	*Professor Solution*	Answer
mutual 1		Find the AC steady-state currents i₁ and i₂.	28k / 128k	15sin(8t-37deg) A, 3sin(8t) A
mutual 2		Find the AC steady-state current i(t).	28k / 128k	3.29cos(4t+9.5deg) amps
mutual 3		Find the AC steady-state voltage v(t).	28k / 128k	3.88cos(4t-166deg) volts

s-domain analysis

For each of the problems in this section: Transform the circuit to the s-domain, use circuit analysis to solve for the desired result in the s-domain, then use the inverse Laplace transform to obtain the time-domain result.

Circuit	Schematic	Problem Statement	*Professor Solution*	Answer
s-domain 1		Find the equation for v_C(t) that is valid for all time t, and sketch a graph of the equation.	28k / 128k
s-domain 2		Find equations for i₁(t) and i₂(t) that are valid for all time t, and sketch a graph of the equation.	28k / 128k
s-domain 3		Find the equation for v_C(t) that is valid for all time t, and sketch a graph of the equation.	28k / 128k
s-domain 4		Find the equation for v_o(t) that is valid for all time t, and sketch a graph of the equation for t = 0 to 8 seconds.	28k / 128k
s-domain 5		Plot v_o(t) for time t = 0 to 10 seconds.	28k / 128k
s-domain 6		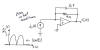Plot v_o(t) for time t = 0 to 15 seconds.	28k / 128k

Driving point impedance

For each of the problems in this section: Express all results as a ratio of polynomials in s, using a unit coefficient for the highest order denominator term.

Circuit	Schematic	Problem Statement	*Professor Solution*	Answer
imped 1		Find the driving point impedance Z(s) at terminals A-B, C-D, and A-C. Comment on any patterns you see in your results.	28k / 128k
imped 2		Find the driving point impedance Z(s) at terminals A-B, C-D, A-C, and B-D. Comment on any patterns you see in your results.	28k / 128k

Transfer function of a circuit

For each of the problems in this section: Express all results as a ratio of polynomials in s, using a unit coefficient for the highest order denominator term.

Circuit	Schematic	Problem Statement	*Professor Solution*	Answer
transfer 1		Find the transfer function H(s) for for terminals A-B as input and terminals C-D as output.	28k / 128k
transfer 2		Find the transfer function H(s) for for terminals C-D as input and terminals A-B as output.	28k / 128k
transfer 3		Find the transfer function H(s) using the proportionality method.	28k / 128k

Pole-zero diagrams

Circuit	Schematic	Problem Statement	*Professor Solution*	Answer
pzd 1		Draw the pole-zero diagram of F(s).	28k / 128k
pzd 2		Draw the pole-zero diagram of F(s) given the time-domain form f(t).	28k / 128k
pzd 3		Find the pole-zero diagram for each transfer function.	28k / 128k
pzd 4		Find the pole-zero diagrams for: H(s) = Vout(s) / Vin(s), Zin(s), and Zout(s).	28k / 128k
pzd 5		For each pole-zero diagram, find H(s) expressed as a ratio of two polynomials in s, with the highest order denominator coefficient as unity; find H(s) expressed as a sum of basic terms (do partial fraction expansion)	28k / 128k

Transfer function realization

Circuit

Schematic

Problem Statement

Professor Solution

Answer

tfr 1

Find four different circuits to realize H(s) as follows:

	Passive network: resistor(s) and inductor(s)
	Active network: resistor(s) and inductor(s)
	Passive network: resistor(s) and capacitor(s)
	Active network: resistor(s) and capacitors(s)

Use "reasonable" component values.

Verify your finished circuits by evaluating their responses at H(0) (DC) and H(¥) (high frequency).

28k / 128k

There are several possible circuit topologies, and the component values are not unique.

tfr 2

Design a circuit based on resistor(s), capacitor(s), and op amp(s) that realizes H(s).

Use "reasonable" component values.

Verify your finished circuits by evaluating their responses at H(0) (DC) and H(¥) (high frequency).

28k / 128k

There are several possible circuit topologies, and the component values are not unique.

s-plane and AC steady state

Circuit

Schematic

Problem Statement

Professor Solution

Answer

s-plane 1

	Plot the magnitude of the sinusoidal steady state response H(jw) for w = 0 to 100 rad/s.
	Draw the pole zero diagram of H(s).
	Comment on the relationship between your two previous results.

28k / 128k

s-plane 2

	Plot the magnitude of the sinusoidal steady state response H(jw) for w = 0 to 200 rad/s.
	Draw the pole zero diagram of H(s).
	Comment on the relationship between your two previous results.

28k / 128k

s-plane 3

Given the transfer function of a circuit and its sinusoidal input excitation, find the output signal in the sinusoidal steady state.

28k / 128k

s-plane 4

Given the transfer function of a circuit, determine the frequency (or frequencies) at which the gain is 25.

28k / 128k

29 and 45 rad/s

Bode plots

Circuit

Schematic

Problem Statement

Professor Solution

Answer

bode 1

	Construct the Bode straight-line approximation magnitude and phase plots of H(s) using the paper-and-pencil method.
	Make computer-generated plots of magnitude and phase response of H(s).
	Compare and comment on your results.

Part 1 - magnitude plot:
28k / 128k

Part 2 - phase plot:
28k / 128k

bode 2

	Construct the Bode straight-line approximation magnitude and phase plots of H(s) using the paper-and-pencil method.
	Make computer-generated plots of magnitude and phase response of H(s).
	Compare and comment on your results.

Part 1 - magnitude plot:
28k / 128k

Part 2 - phase plot:
28k / 128k

bode 3

	Find a transfer function H(s) whose Bode magnitude plot matches the given straight-line approximation.
	Check your work by making a computer-generated plot of the magnitude response of your H(s).
	Compare and comment on your results.

28k / 128k

For questions or comments regarding this web contact:
Last updated: 03/10/05.