CSSE 230
Editor Trees Solo Programming Assignment

Milestones

1	(50 pts)	Implement and test: `add(char c, int pos)`, `add(char c)`, and `get(int pos)`, plus (for testing purposes) `EditTree()`, `EditTree(char)`, `slowHeight()`, `slowSize()`, `ranksMatchLeftSubtreeSize()`, `toRankString()`, and `toString()`. The tree does not have to be height-balanced, only to pass the unit tests.
2	(70 pts)	All of the above, but now the tree must be kept height-balanced. Plus: `EditTree(EditTree e)`, `fastHeight()`, and for testing, `toDebugString()`, `totalRotationCount()`, and `balanceCodesAreCorrect()`.
3	(160 pts)	Final submission of all code: all of the above, plus `delete(int pos)`, `EditTree(String s)`, and `get(int pos, int length)`. Includes correctness, efficiency constraints (see below), and style.

Overview

EditorTrees is the major course project, as described in the syllabus.

You will work on this assignment in groups of two (or three for the one odd group). Please use the link on our class's Moodle page to accept the project invite, and check CATME for your groups.

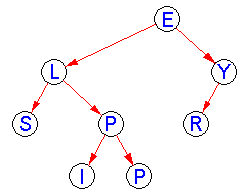
In this project you will write methods of a class that could be the "behind the scenes" data structure used by a text editor. Each piece of text will be represented as a height-balanced tree with rank and balance codes. Each node contains a single character. Note that an EditTree is not an AVL tree in the traditional sense, since the order of nodes reflects their position within the tree's text rather than an alphabetical ordering of the characters in the tree. To repeat, this is not a Binary Search Tree, it is a balanced-tree implementation of Lists. For example, the text "SLIPPERY" could be represented by the height-balanced tree at the right.

You will focus on data structures and algorithms. You will not write a user interface with this.

Learning Outcomes

Implement a complex data structure and associated algorithms.

More than any other in this course, this project will require you to design your algorithm ahead of time.

Make effective use of your debugger.

Read algorithm descriptions and use them as a basis for your Java code.

Requirements

You must implement all of the methods whose stubs are in the provided EditTree code. Each method that creates or modifies a tree must leave all trees height-balanced. Most of the requirements (including big-oh bounds on worst-case runtime) are presented to you as comments in that code, because context should make them clearer.

These methods must run in O(log N) time, where N is the size (number of nodes) in the largest tree involved in the operation.

add(char c)
add(char c, int pos). It is particularly important to get this one right in milestone 2, as later unit tests build on it.
delete(int pos)
get(int pos)
fastHeight()

These methods must run in O(N) time, where N is the size (number of nodes) in the tree involved in the operation.

toString( )
EditTree(String s)
EditTree(EditTree e)
slowHeight()
slowSize()
ranksMatchLeftSubtreeSize()
balanceCodesAreCorrect()

The following required method is for grading purposes only: int totalRotationCount(), which returns the total number of rotations done in this tree since the tree was first created. A single rotation adds 1 to this count, a double rotation adds two.

Be sure to commit your versions often as you go, and mark your Milestone 1 and Milestone 2 submissions clearly in your commit log, so that we will know which one to grade!

Design Considerations

Certain operations would be really easy to implement if you didn't care about efficiency.

In order to do certain operations efficiently, like add() and get(), you already know that you need extra data in your nodes, a balance code. Here is another data member that is needed to implement the List interface efficiently: rank. First, some background. To access a node by index, that each node needs some way of figuring out that index it is in the tree. It would be nice if each node stored its index, but there is one problem: if you do an add(), then the index of every node after the added node would have to be incremented, and this takes longer than O(log n) time. Instead, we'll have each node store its own rank. Rank is defined as the 0-based index of the node within its own subtree (the one rooted at that node). If you check this, you'll see that it also happens to be the size of the node's left subtree. Ranks can be used to compute indices as you move down the tree, and can be updated after an add or delete in O(log n) time. Your code will need to:

Use rank to efficiently determine whether to go left or right to find an index.
Increment the ranks of certain nodes as you go down the tree in .add().
Update the ranks of 1-2 nodes when certain rotations are done.

You should also consider whether or not you want to add yet more data beyond balance code and rank:

Leaf nodes could have NULL_NODEs as children (generally a good idea).
Each node could store a pointer to its parent. I've solved this project both with and without it, and find it easier to do without it. Knowing a parent can be helpful, but it's just one more thing you need to update when inserting/removing a node and it's a pain to debug.

Another decision you'll need to make is how to traverse your tree. For instance, when adding a node, you'll need to walk down the tree to figure out where to insert it, and back up to figure out if it needs to be rotated. How will you do this traversal? It may depend on the method. Some options:

Use recursion - it's most natural to just add code to the recursive method after it makes its recursive call
Add a parent pointer to each node
Loop, and maintain your own stack of nodes traversed, so you can find your way back up.

Finally, you'll notice that Node isn't an inner class of EditTree, because both classes can be fairly large. You can choose where to do your work.

A Quick and Dirty Visualization program

Your repository contains a package called debughelp. In that package are two classes, developed by CSSE230 student Philip Ross, that display the tree nicely in a window, complete with rank and balance code. You may use them if you like. The package also contains a sample of the output from the program, and a README with instructions about what extra fields and methods you'll need to add if you choose to use it. Many students have found it worth their time to use!

Hints and Process

When I wrote my solution this last time, here is what I did. The times are shorter than yours will be since I have solved this before, but I want you to have some sense of relative times in the milestones:

Milestone 1 (total time ~1:10)
1. (30 min) Read the specification and the starting code and took notes of key ideas.
2. Wrote the Node constructors.
3. Wrote toString() and passed the first couple unit tests.
4. Wrote the two add() methods using rank to figure out where to insert the element (drawing several example trees, like in session 15). Simple since ignored balance codes and rotations for now. Earned a few unit test points, then wrote toRankString() and earned the rest.
5. Noted that the first add() method is really a special case of the second so just had the first one call the second one. (An alternative is to implement the first one as a warmup to the second one.)
6. Add() is currently O(n) since it isn't height-balanced yet.
7. Wrote get(pos).
8. Wrote slowHeight() and sizeSize() and integrated the graphical debugger.
9. Wrote the method to verify that ranks are correct.
Milestone 2 (total time ~1:00)
1. I commented out the "stress tests" at the bottom of the Milestone 2 unit tests - they are slow to run until you implement balancing and rotations.
2. When implementing re-balancing and rotations, found it really helpful to pass in a mutable "NodeInfo" object to keep track of the rotationCount and whether the rebalancing should continue as the recursion unwound up the tree.
3. Session 13 material was really helpful here. Drew examples showing each of the rotations in the slides and how to update ranks. Noted that we already wrote singleRotate() on the session 13 quiz.
4. Wrote code to verify that balance codes are correct. Modifying the method to print Nodes where the balance codes were broken was helpful in debugging.
5. I had made a couple of small careless mistakes that I found fairly quickly using the Java debugger.
6. Wrote the EditTree(et) constructor.
Milestone 3 (total time ~1:45)
1. Drew several tree pictures to remind myself that the conditions to continue balancing after a deletion are completely different than they were for add (day 14 examples were helpful here).
2. Got delete() code-complete in 45 minutes, passed most of the tests.
3. Spent a full 45 minutes more tracking down the last couple small bugs in delete that only showed themselves on the later unit tests on bigger trees. Drew several more large trees (like the "tree from day 14 slides") to help trace where my code failed.
4. Wrote the EditTree(string) constructor and the other get() - that one was quick since it could use the first get().

Grading

Correctness is still king. Unit tests will be a large part of the points.

Efficiency is still important. As stated above, some of these operations could be implemented very easily if we didn't care about efficiency. The purpose of this assignment is for you to learn how to implement efficient algorithms for maintaining balanced trees. So correctness is only part of the assignment. Solutions that pass all the unit tests but are inefficient will only earn a small fraction of the points.

Documentation and style do count for something. As you go, please add internal comments to small blocks of code to capture WHY you are writing the code that way. If you put comments later, the temptation is just to say WHAT you did for each line (which can just be determined from the code and is pretty useless, like: node = node.right // move to the right

How do you check if your code is O(log n)? Unless you need to traverse the tree, then at every node navigate either to the left or to the right child. A traversal is when you have to pass down both sides, this type of operation will be O(n). And when you are re-balancing the tree, you should only take one path up the tree, rebalancing as you go and stopping as soon as you can - DON'T create a rebalance() method that traverses the entire tree!

The test files for Milestones 2 and 3 may be updated.

CSSE 230 Editor Trees Solo Programming Assignment