Asymptotic Bounds

Last Updated: 30 Nov 2018

Θ Notation - Asymptotic Tight Bounds

Asymptotic Tight Bounds

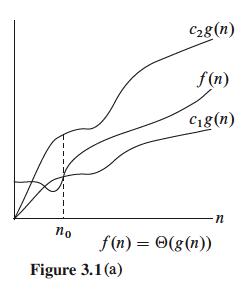
Showing Θ:

  • Method #1 - Find constants n0, c1, and c2

  • Method #2 - Take limit:

 

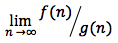
You have shown f(n) ∈ Θ(g(n)):

  • If Method #1 leads to finding the 3 constants
  • If taking the limit in Method #2 leads to a constant c

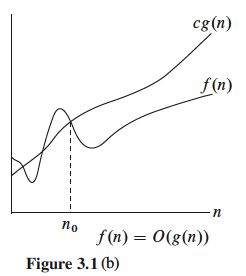
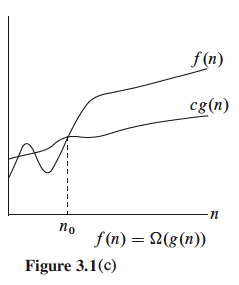
You have shown f(n) ∉ Θ(g(n)):

  • If Method #1 fails to lead to finding the 3 constants
  • If taking the limit in Method #2 leads to zero or infinity

What makes this a tight asymptotic bound?

  • Because f(n) is sandwiched in between c1g(n) and c2g(n)

 

Figure 3-1 a

Cormen 3e 2009 (c)

O Notation - Asymptotic Upper Bound - Not Necessarily Tight

Asymptotic Upper Bound

Showing O:

  • Method #1 - Find constants n0, c

  • Method #2 - Take limit:

 

You have shown f(n) ∈ O(g(n)):

  • If Method #1 leads to finding the 2 constants
  • If taking the limit in Method #2 leads to a constant c, then you have also shown that g(n) is a tight upper bound, i.e., f(n) ∈ Θ(g(n))
  • If taking the limit in Method #2 leads to 0, then you have shown f(n) ∈ o(g(n)), i.e., that g(n) is an upper bound but it is not a tight upper bound

You have shown f(n) ∉ O(g(n)):

  • If Method #1 fails to lead to finding the 2 constants
  • If taking the limit in Method #2 leads to infinity

 

 

Figure 3-1 b

Cormen 3e 2009 (c)

 

Ω Notation - Asymptotic Lower Bound - Not Necessarily Tight

Asymptotic Lower Bound

Showing Ω:

  • Method #1 - Find constants n0, c

  • Method #2 - Take limit:

 

You have shown f(n) ∈ Ω(g(n)):

  • If Method #1 leads to finding the 2 constants
  • If taking the limit in Method #2 leads to a constant c, then you have also shown that g(n) is a tight lower bound, i.e., f(n) ∈ Θ(g(n))
  • If taking the limit in Method #2 leads to infinity, then you have shown f(n) ∈ ω(g(n)), i.e., that g(n) is a lower bound but it is not a tight lower bound

You have shown f(n) ∉ Ω(g(n)):

  • If Method #1 fails to lead to finding the 2 constants
  • If taking the limit in Method #2 leads to zero

Figure 3-1 c

Cormen 3e 2009 (c)