CSSE 230
Data Structures and Algorithm Analysis

Small Programming HW 4 - 47 points

To Be Turned In

StringHashSet implementation. You will be implementing a HashSet using separate chaining. It implements many of the methods from Java's Set interface.

Additionally:

• You will use an array for internal storage, and will grow the array when lambda gets too big. (Don't use an ArrayList since it won't grow at the right time.)
• It only needs to work for Strings.
• You will implement a method to compute the String hash code.
• You will also implement a toRawString function that dumps out the array of LinkedLists without formatting - this is to make sure it is putting everything in the right place.
• You will implement many other methods. I did them in the order they appeared in the file, and the tests for later ones assume you passed the tests for the earlier ones. For example, to test remove(), we need to be able to add values first.
• One cannot insert null
• Java's HashSet has an initial capacity of 16 and rehashes when lambda reaches .75. To force more collisions earlier, we will use an initial capacity of 5, and rehash when lambda reaches 2.
• (Optional: for 5 bonus points) The most challenging (fun) part of this was writing an iterator, since it needed to traverse a bunch of possibly empty linked lists. Once you have an iterator, it made some other things (toString and rehashing) easier. But I recognize you are busy with your project, so am making the iterator optional, and worth a few bonus points as a reward if you get it working on your own.  

When you finish, upload your .java file to this Moodle assignment.

Optional practice problem - not to be turned in.

(0 points) Start with the following Binary Search Tree:

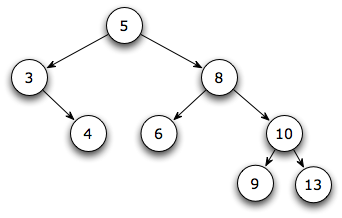
See the hint at the end!

1. Is this an AVL tree? ____ If not, rearrange it so that it is height-balanced.
2. Draw the tree after insertion of a node containing 11, using the usual BST insertion algorithm.
3. Is the new tree AVL? ______ If not, name the node where the rotation should be done, according to the algorithm from class. ______ Single or double rotation? ____________ If you need to do a rotation, draw the resulting tree.
4. Delete the element 5 from the original tree (not the one from part c), using the BST deletion algorithm described in class and in the textbook. Draw the new tree.
5. Is the new tree AVL? ______ If not, name the node where the rotation should be done, according to the algorithm from class. ______ Single or double rotation? ____________ If you need to do a rotation, draw the resulting tree.
6. Is your new tree (if any) AVL? ______ If not, name the node where the rotation should be done, according to the algorithm from class. ______ Single or double rotation? ____________ If you need to do a rotation, draw the resulting tree.
7. Add the element 5 to the tree from part (f) using the BST algorithm. Draw the new tree.
8. Is the new tree AVL? ______ If not, name the node where the rotation should be done, according to the algorithm from class. ______ Single or double rotation? ____________ If you need to do a rotation, draw the resulting tree.
9. Add the element 12 to the tree from part (h). Draw the new tree.
10. Is the new tree AVL? ______ If not, name the node where the rotation should be done, according to the algorithm from class. ______ Single or double rotation? ____________ If you need to do a rotation, draw the resulting tree.
11. Add the element 7 to the tree from part (j). Draw the new tree.
12. Is the new tree AVL? ______ If not, name the node where the rotation should be done, according to the algorithm from class. ______ Single or double rotation? ____________ If you need to do a rotation, draw the resulting tree.

Hint: In my solution, for all the sub-parts together, I did three single rotations and no double rotations. The first four leaf nodes in my final tree were 3, 5, 7, and 9. (In my first attempt, I misread part d) and deleted from the tree in part c) rather than the original tree. With that mistake, for all the sub-parts together, I did two single rotations and one double rotation and the first four leaf nodes in my final tree were also 3, 5, 7, and 9.)