CSSE 230
Data Structures and Algorithm Analysis
Homework 10 - 47 points
To Be Turned In
Upload your solution to the Moodle assignment.
- (15 points). Weiss Exercise 19.7.
Prove it by strong induction on the number of internal nodes in the
tree. The
induction assumption applies to the left and right subtrees. This
exercise is based on the discussion from pages 644-647 (beginning of
section 19.3) and Exercise 19. I restate it in terms of Extended Binary
Trees (EBTs), because the definition is a bit more precise than the one
in the middle of page 647. An EBT T either consists of one external
node, or it consists of an internal node (the root) and two subtrees, TL and TR, each of which is an EBT. If T
is an EBT, then its internal path length,
IPL(T) is the sum of the depths of all of the internal nodes of T.
Similarly, its external path length,
EPL(T) is the sum of the depths of all of the external nodes of T.
For example, if T is the EBT shown here, then IPL(T) = 0+1+1+2+3 = 7,
EPL(T) = 2+2+2+3+4+4 = 17. Can you figure out the relationship between
IPL(T) and EPL(T)? (Think about it now)
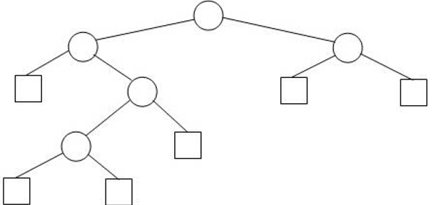
Answer: EPL(T) = IPL( T) + 2*IN(T). It's easy to see that this formula
is true for this tree. Your
job is to show that it is true for all
extended binary trees. Use strong induction to show
that
for any EBT T, EPL(T) = IPL( T) + 2*IN(T). All induction is
over some integer, in this case it is the nunber of internal nodes.
Be sure that you
explain what you are
doing. You may introduce any new notation that may be helpful.
- (12 points) Solve the recurrence relations below. Indicate
which strategy you are using and show your work. Big-theta or exact
answer required? Big-theta. On any problem where it is appropriate to
use the Master Theorem, big-theta is sufficient (you can't get better
from the theorem). But if the master theorem doesn't apply for a
certain problem (hint, hint), you'll have to use another technique like
telescoping, or filling out a table and doing guess and check. And then
you'll have an exact answer anyway on your way to getting big-theta. So
write the exact answer too as part of your solution.
- T(1) = 1, T(N) = 2 T(N/4)
+ N0.5
- T(1) = 1, T(N) = T(N
- 2) + 2, assuming N is odd.
- T(1) = 1, T(N) = 3 T(N/2)
+ 2N
- (10 points) Use a recurrence relation to show that the
running time of the
printPreorder method
in Figure 18.22 is O(N). You may assume
that the tree is perfect (i.e., full, balanced, and size 2k
- 1 for some integer k).
- (10 points) Weiss Exercise 8.14[8.14]. Duplicates are allowed and
should be accounted for in the median computation: for example, if
A = [1,3,3] and B = [2,3,3], then the answer should be the median of
[1,2,3,3,3,3], which is 3.
You don't need
exact Java code, but explain your algorithm in enough detail to
convince us it works in O(Log N) time. This will require some insight -
don't leave it to the last minute!
For Your Consideration
These problems are for you to think about and convince
yourself that you could do them. It would be good practice to actually
do them, but you are not required to turn them in.
- Weiss exercise 6.4 [6.4].
