CSSE 230
Data Structures and Algorithm Analysis
Homework 9 - 45 points
Reading (optional)
In our textbook (link at top of Moodle page), read 3.1-3.3, 3.5-3.8 (and more*).
This is all of chapter 3 (sorting) except 3.4. Section 3.4, shellsort, is optional but interesting (the runtime isn't O(n2) or
O(nlogn), but O(n3/2)...).
Plus, section 9.9 isn't required but may be useful to you when doing GraphSurfing Milestone 2.
To Be Turned In
Submit to the drop box.
- (23 points). Average-case analysis of unsuccessful search on a naive binary search tree (i.e., NOT
self-balancing. Note: we assume such trees are created using only insertions, not deletions.)
- (Adaptation of Weiss Exercise 19.7.) For an extended binary tree (EBT) T, you know already that
internal path length IPL(T) is the sum of the depths of all of the internal nodes of T.
Similarly, the external path length,
EPL(T), is defined as the sum of the depths of all of the external nodes of T.
Determine a formula relating EPL(T) and IPL(T).
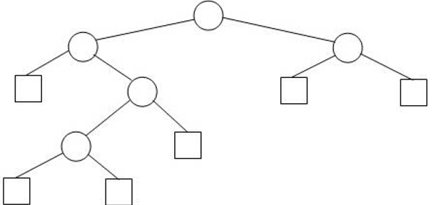
Hints: An example of this fact is given by the tree in the following picture: note that IPL(T) =
0+1+1+2+3 = 7, and
EPL(T) = 2+2+2+3+4+4 = 17. How much do they differ? Is that related to the number of internal nodes
in the tree? How?
Try to determine a formula and to verify it with two more trees:
first, a tree with a single internal node and two external nodes, and second, another tree of your
choosing.
To turn in:
- (6 pts) Your formula
- (6 pts) Calculations on 3 trees (the given one, the tiny one, and another of your choosing)
showing that the formula works for each.
- (3 pts) A brief explanation of why this formula makes sense.
- (0 pts; optional) Prove the formula by strong induction on the number of internal nodes on
the tree.
-
Suppose that an unsuccessful search (for a value not in the tree) is equally likely to end in any of the external nodes of the tree. Given this assumption, the successful-search analysis from class, and the result of your proof from (a), what can you say about the average-case big-O running time of an unsuccessful search on a naive BST? Briefly explain your answer.
answer.
- (12 points) Solve the recurrence relations below. Indicate
which strategy you are using and show your work. Big-theta or exact
answer required? Big-theta. On any problem where it is appropriate to
use the Master Theorem, big-theta is sufficient (you can't get better
from the theorem). But if the master theorem doesn't apply for a
certain problem (hint, hint), you'll have to use another technique like
telescoping, or filling out a table and doing guess and check. And then
you'll have an exact answer anyway on your way to getting big-theta. So
write the exact answer too as part of your solution.
- T(1) = 1, T(N) = 2 T(N/4)
+ N0.5
- T(1) = 1, T(N) = T(N
- 2) + 2, assuming N is odd.
- T(1) = 1, T(N) = 3 T(N/2)
+ 2N
- (10 points)
You are given two arrays, A and B. Each is sorted and contains N elements.
Give an O(log N) algorithm to find the median of all 2N elements in the union of A and B.
Duplicates are allowed and should be accounted for in the median computation: for example, if
A = [1,3,3] and B = [2,3,3], then the answer should be the median of [1,2,3,3,3,3], which is 3.
You don't need exact Java code, but explain your algorithm in enough detail to
convince us it works in O(Log N) time. This will require some insight -
don't leave it to the last minute!
For Your Consideration
These problems are for you to think about and convince
yourself that you could do them. It would be good practice to actually
do them, but you are not required to turn them in.
- Weiss exercise 6.4 [6.4].
