CSSE 230
Data Structures and Algorithm Analysis
Homework 6 - 77 points
Reading (optional)
In our textbook, read 7.1 - 7.4 (the zybooks "assignment" called "Reading for HW5"), and chapter 5 (the zybooks "assignment" called "Reading for HW6").
If you choose to study red-black trees and want more, feel free to read 7.5 - 7.8.
There are many ways to implement AVL trees, and what the book presents is little different than what we'll do, so
I want to help you make connections. First, you should noticed that the balance factor (1, 0, -1) is equivalent
to
our balance codes (LEFT, SAME, RIGHT). But we actually don't need to store actual heights in each node - after
rotation, we can find the balance codes directly from the previous balance codes - and they are often SAME! The
less info we track in each node, the easier it is to keep updated. Furthermore, our methods return Nodes, to be
used by the parent in the recursion to set their children (like left = left.insert(x) we used for
BST insert),
so we don't need parent pointers, won't use while loops, and don't have to treat the root as a special case. For
these reasons, the algorithms you will write for tree balancing will follow what we did in lecture, which are
simpler than the text's. (And of course, we are implementing a height-balanced implementation of the List
interface, using ranks, so our trees won't be BSTs.)
Double rotations do by two names: a double rotation's direction is named by the second rotation's direction.
So a left-right rotation and a double-right rotation are the same.
(Likewise, a right-left rotation and a double-left rotation are the same.)
Summary: the book's 4 imbalance and rotation cases are the same, and I think you'll find the animations and
exercises to be valuable! But you don't need to pay attention to their actual code.
To Be Turned In
Submit
to the dropbox, except the programming problems at the end which go to the repo. You may earn or use a late day
for this assignment. Like all written assignments, this is an
individual assignment. You may discuss it with others, but you should
write (and code) your answers yourself.
- (10 points) Let S(H) denote the minimum number of nodes
in a height-balanced tree of height H. Prove that S(H) = Fib(H+3) - 1 for
all H ≥ 0 by
induction.
Hint: We observed in class that S(H) = S(H-1) + S(H-2) + 1. Use this
observation in your proof. (If you missed this observation, you should
review it, asking for help if needed, until you convince yourself this
is true.) Here are a couple of supplementary online resources on
induction that I like: (1) Video demo
and web page (this
page does a few examples, and explains more about why is works with
a couple of cool examples showing what happens if you
use math induction incorrectly!)
- (10 points)
Height-balanced (AVL) trees guarantee that the difference in height between subtrees is limited to at
most one. But how different could the relative sizes of AVL subtrees be? Answer this question by
considering an AVL tree of height H, where the root has left subtree TL of as small a size as
possible and right subtree TR of as large a size as possible. Compute formulas (in terms of H)
for the sizes of TL and TR, and take the ratio N(TR)/N(TL) of
their sizes. Then take the limit of this ratio as H increases. Is the ratio of sizes limited to a constant,
or can it grow arbitrarily large?
-
(12 points) Fill in the following table. Be
very careful to get the exact values. Most of the
credit will be for the last column. Don't use the AVL approximation
formula (H < 1.44log(...)). Instead, draw trees and look for the
patterns, like we did on day 13 in class.
Feel free to include explanations of your answers.
correct_answer → full_credit. wrong_answer +
no_explanation → no_credit.
1/2 point for each entry in the
first two columns, and 2 points each for each entry in the last column.
| n
|
Height of shortest
binary tree with n nodes |
Height of tallest binary
tree with n nodes |
Height of tallest AVL
tree with n nodes |
| 7 |
2 |
6 |
3 |
| 8 |
|
|
|
| 370 |
|
|
|
| 17000 |
|
|
|
| 50000 |
|
|
|
- (25 points) More tree practice! Checkout the TreePracticeHW5 project from your Git repository.You will write three methods
for Binary Trees. Like the last homework, the trick to these is to add
parameters or multiple return values (through your own custom class) to
your recursive helper method. Commit
your work to Git as you make progress and when you finish.
- getSumOfHeights.
Find the sum of the heights of every node in the tree. This is an
interesting problem if you want to do it efficiently, meaning in O(n)
time. Just calling height() on each node will give the correct answer,
but it duplicates a lot of work and leads to an O(n log n) algorithm.
Could you somehow combine finding the height with finding the sum of
the heights in your method? Hint: don't use a field - that has a side
effect of modifying each node. Instead, use either multiple return
values (which I think is clean) or mutable parameters to do the
trick. Hint: I solved this problem step-by-step in a couple
Session 12 videos.
- isHeightBalanced.
Determine if the given tree is height-balanced, using the definition given in class.
This is an another interesting problem. For full credit, do it efficiently, meaning in
O(n)
time. Like the previous problem, just calling height() on each node will give the correct answer,
but it duplicates a lot of work and leads to an O(n log n) algorithm.
Could you somehow combine finding the height with finding if the node is height-balanced
in your method? See the hint on the previous problem.
- Full tree
constructor. Create a full tree of Integers whose leaves
have the given depth, and where every node is labeled with its
own depth. (Reminder: Full trees are those in which all the leaves have the same depth.)
It is good experience to know how to build a whole tree by calling
a single method.
-
(20 points) Checkout the PreorderBuildTree project from
your Git repository. In this problem, you'll create another Binary Tree
constructor, one that constructs a Tree with Character data from two
pre-order lists: a string of data and a string of children. For
example, t = BinaryTree("abc", "200") would create a full tree of
height 1 with root = a and two children b and c, and t =
BinaryTree("cbad", "2L00") would create the minimum height-balanced
tree of height 2, with an in-order traversal of "abcd".
As a larger example, this tree was built from the strings, "ARGEDFKJHWS" and "R22200LL0L0":
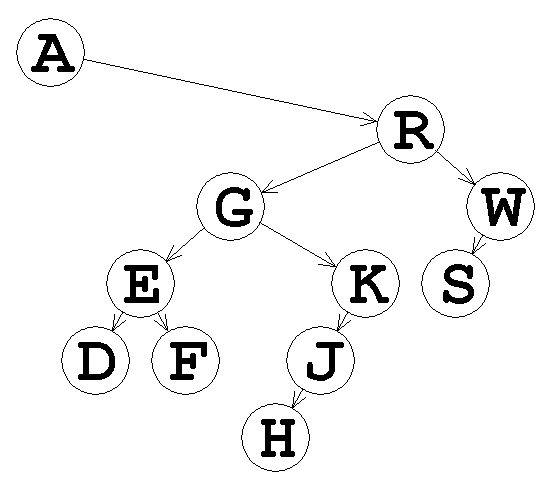
This format should sound familiar - see HW3 and its solution
for more details. Note that this can construct any binary tree of
characters, not just BSTs. I am posting two hints here, but I strongly suggest that you try to develop an algorithm first before referring to them.
Other problems for your consideration
6.31[6.17], 6.37[6.22], 7.3[7.3], 7.4[7.4],
7.23[7.19], 7.29
