(20 points) Calculate the exact average-case time complexity of binary search. You may use any standard implementation of binary search, e.g., textbook, wikipedia, etc. Only consider successful searches (where the item we are looking for is actually in the array) and assume all elements are equally likely to be the one we are searching for.
- Complete this for N=7 elements in the array.
- Complete this for N=15 elements in the array.
- Complete this for N = 2k - 1 for some integer k ≥ 0, generalizing from what you found in (a) .
Hint: For each i, count how many of the array elements will be found after binary search examines exactly i array elements. (For example, the middle element is the only one to be found after examining one array element, and there are two elements that can be found after examining two array elements.) Then sum over all and divide to find the average. For the generalization, you'll use a summation. You need to convince me somehow that your summation is correct, perhaps using a table or words. Once you have done that, then you may find the following formula useful:
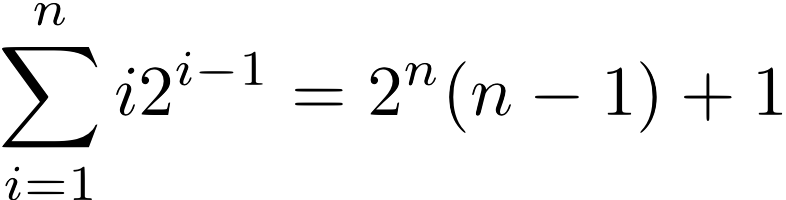
After you have done that, you'll get a messy expression with lots of terms in it. Take the limit as n gets large so some terms go to zero. You'll end up with a much simpler expression that should be clearly between 1 and log(n), like we said in class.
The interesting question we are trying to answer here is how much smaller is the average-case analysis compared to the worst case analysis you can find in your text- book.