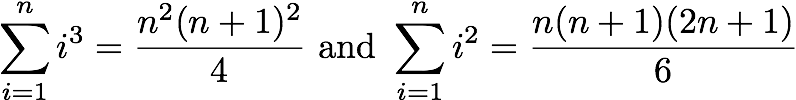CSSE 230
Data Structures and Algorithm Analysis

Homework 4  -  22 points

Upload your solution to the Moodle assignment.

The following formulas for series sums may be helpful:

[Numbers in brackets] are problem numbers from the third edition of the Weiss textbook.

1. (8 points) Weiss Problem 5.21 [5.16]. You only need to do the analysis, not an implementation. This one is more complex than previous problems of this type. As with our analysis of the cubic algorithm for MCSS in class, you should first derive a (closed-form, no-summation notation) formula for the exact number of times that the sum++ statement executes. Be sure to explain what you are doing, not just write equations. Use your derived formula to state a big-Theta estimate; you can use the usual shortcut of dropping lower-order terms and constant factors only at this last stage.

   You do not have to implement and run the code.

2. (7 points) It is useful to have a unique representation of binary trees that can be written compactly. For simplicity, we assume that each node of the tree will contain one Character. We represent a tree by a pair of strings, which I call chars and children. The chars is a pre-order listing of the contents of the nodes. The children string tells about the children of the corresponding node from chars as follows:

   2	The node has two children.
   0	The node has no children.
   L	The node only has a left child.
   R	The node only has a right child.

   For example:

   chars = "+a*-bcd"; children = "2022000";
   represents the tree in Weiss Figure 18.11 (a)

   chars = "7215349"; children = "220LR00";
   represents the tree in Weiss Figure 19.4 (a).

   1. What are the values of chars and children for the tree below?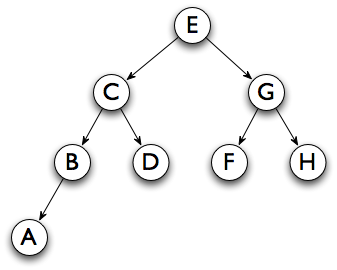

      

   2. For a different tree we have:

       chars = "THEQUICKBROWN";
      children = "2R220002R0RL0";
      

      Show the order of the nodes in an in-order traversal of the tree.

3. (7 points) Hint: use the given info to draw the tree!

   THEQUICKLAZYFOX is the pre-order traversal of a tree (one character per node).

   QIUCEHLAZKFYTXO is the in-order traversal of the same tree.

   What is the order of the nodes in the level-order traversal of this tree?

For Your Consideration

These problems are for you to think about and convince yourself that you could do them. It would be good practice to actually do them, but you are not required to turn them in.

• Weiss Problem 3.15 [3.12]

• This problem is inspired by Weiss exercise 5.11 [5.8], but is different. That problem examines the efficiency of computing X^N, where X is a double value and N is an integer. That algorithm is O(N). It turns out we can do a lot better; there is an algorithm that is O(log N). Write and test code that does this.

  Hint: Base your algorithm on the binary representation of N. For example, X¹¹ = X¹*X²*X⁸ (Note that 11 has one-bits representing 1, 2, and 8). So you can write N as a sum of powers of 2. Start with power=X, and keep squaring power to get the original X to those powers of 2. Only multiply X⁽²ⁱ⁾ into the product if the ith bit of the binary representation of N is 1. Your program should ask the user for X and N, and print X^N.

  Another hint: It is probably easier to do this recursively.

  You can just write the code out by hand if you wish, but I recommend actually coding and testing it.

• Weiss Exercise 6.33 [6.18]. Your program should read strings (one per line) form standard input, and write Strings (one per line) to standard output. The alphabetical part of the sort should ignore case. Hint: Use a two-argument overloaded version of java.util.Collections.sort().

  Sample Run:

  Enter the strings, one per line (CRTL Z to end):
  Come
  and
  sit
  by
  my
  side,
  if
  you
  love
  me
  Do
  not
  hasten
  to
  bid
  me
  adieu
  Just
  remember
  the
  Red
  River
  Valley
  And
  the
  cowboy
  who
  loved
  you
  so
  true
  SORTED LIST OF STRINGS:
  by
  Do
  if
  me
  me
  my
  so
  to
  and
  And
  bid
  not
  Red
  sit
  the
  the
  who
  you
  you
  Come
  Just
  love
  true
  adieu
  loved
  River
  side,
  cowboy
  hasten
  Valley
  Remember