CSSE 230
Data Structures and Algorithm Analysis

Homework 2 (58 points)

To Be Turned In

Upload your solution to the Moodle drop box. See submission instructions in HW1.   After you have submitted, click on the uploaded submission to verify that your submission was successful.

A single late day may be used or earned for each homework assignment: you must turn in all parts early to earn a late day; if you turn in any part late, you will use a late day.

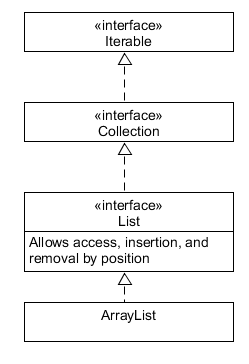
1. (10 points) Using the official javadoc, draw a UML diagram of the Collections framework. Add whatever notes you find helpful. Include at least these classes/interfaces: ArrayList, Collection, ConcurrentSkipListSet, HashSet, Iterable, LinkedHashSet, LinkedList, List, PriorityQueue, Queue, Set, SortedSet, Stack, and TreeSet. These are the main ones; we skipped most of the concurrent/blocking structures, and some special-purpose ones. Note that the map ADT (AbstractMap, TreeMap, and HashMap) aren’t connected to the others: they form their own hierarchy that is so close to that for Sets, that it isn't worth you writing (although we expect you to know and use Maps). Hints: 1. Most relationships are that of an interface extending or a class implementing an interface - use dotted lines there. There is only one example of inheritance - use a solid arrow there. 2. A class may implement multiple interfaces - there is one example of that here. 3. Here is the top of the hierarchy - copy this pic and skim each of these interfaces and class in the javadoc to get started. 4. I just started with the ArrayList javadoc and looked for the required classes/interfaces (finding Iterable, Collection, and List), and then looked at each of those to see which one was a subinterface and which was a superinterface. 5. Feel free to do this with a partner, but you must each submit one copy.   

2. (8 points). Use the formal definition of big-Oh (see Weiss section 5.4) to show that 2N² + 3N + 8 is O(N²). That is, find appropriate constants N₀ and c, and show that they work.
3. (12 points) Let T₁(N) = O(F(N)) and T₂(N) =O(F(N)). Consider the following 4 statements:
   1. T₁(N) + T₂(N) = O(F(N))
   2. T₁(N) - T₂(N) = O(F(N))
   3. T₁(N) / T₂(N) = O(1)
   4. T₁(N) = O(T₂(N))
   For each of these statements: if the statement is always true, explain why using the N₀ and c idea from the formal definition of big-Oh. [Hint: the given bounds on T₁ and T₂ tell you something about the existence of an N₀ and c for each of those functions: we could call these numbers N₀₁, c₁, N₀₂, and c₂] If the statement can be false, give a counter-example: an example of specific functions T₁ T₂, and F for which it is false. (Hints: For algorithm analysis we assume that all the functions have non-negative values; an algorithm can’t execute in negative time.  Note that the use of big-O instead of big-theta here is intentional; some of the answers would be different if big-theta was used instead. Also, exactly two of the above statements are true.)
4. (6 points) In asymptotic analysis, it's very useful to know if the base of a logarithm mattters.
   1. Is it true that log₂(n) is θ(log₁₀(n))? Justify your answer. (Hint: use one of the logarithm formulas!)
   2. Is it true that 10ⁿ is θ(2ⁿ)? Justify your answer.
5. (12 points) For each of the following four code fragments, first give the exact number of times the "sum++" statement executes in terms of n. Then use that to give a Big-Theta running time (by ignoring the low-order terms).

   1. for (int i=0; i <= n+2; i++) {
         for (int j=0; j < n * n; j++) {
             sum++;
         }
      }

   2. for (int i=0; i < n; i++) {
         for (int j=i; j < n; j++) {
             sum++;
         }
      }

   3. You may assume that n is a power of 2.

      for (int i = n; i > 0; i /= 2) {
         for (int j = 0; j < i; j++) {
             sum++;
         }
      }
      

   4. for (int i=n; i >= 1; i = i / 2) {
         sum++;
      }

6. (10 points) Sometimes we give you an algorithm to solve a problem and you figure out how to make it happen in code. This, however, is your first "algorithm design" homework problem of the quarter:

   You have a sorted array a of increasing integers. Give an efficient algorithm that returns true if and only if an integer i exists such that a[i]=i.

   What is the running time of your algorithm?

   You may assume that the array has no duplicate entries, and therefore is strictly increasing. I.e. a[j-1] < a[j] for all j with 0 < j < a.length. You may not assume that all of the integers in the array are non-negative, because then the problem would be boring.

   Show your algorithm (either a Java method or pseudo-code) and the results of your analysis. Obviously you should try to come up with an efficient algorithm; most of the credit for this problem will be based on your algorithm's efficiency. (Think about it carefully—is O(N) "efficient" for this task? Anyone can write a loop from 0 to a.length.)

   Hint: while your goal is to produce pseudocode, algorithm design usually starts with sketching out some small examples and testing informal algorithm ideas on them, modifying them as needed, until you get something that works. For your small example, you could pick a small array of 7 ints, starting with a few negative numbers and increasing from there. Above them, write the indices 0,1,2,3,4,5,6 so you can see how a[i] compares with i. You may want to tweak your first example so that the method would return true, for example, let a[5]=5.