If a is a square matrix,
a call to
det(a)
returns the determinant of that matrix (often written by Mathematicians
as |a| ); otherwise det(a)
throws an IllegalArgumentException.
The determinant is calculated recursively using the �Laplacian expansion�
method of minors and cofactors.
http://mathworld.wolfram.com/DeterminantExpansionbyMinors.html
http://www.richland.cc.il.us/james/lecture/m116/matrices/determinant.html
As an example, if we expand along a row for the 3x3 case, we get
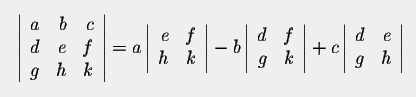
How to implement the det method
Your public method should call a recursive private method that does the actual determinant calculation, calling itself recursively to find each "minor" determinant after "crossing out" a row and column. The temptation for one of the arguments to the recursive calls is to copy the matrix itself, removing the crossed-out row and column. If the matrix size (N) is large, this is a very time-consuming operation – O(N2) for each recursive call.
Instead, we can pass the original matrix to all of the recursive calls, along with two sets of integers that keep track of the "non-crossed-out" rows and columns. Before making a recursive call, we can copy the two sets, remove the appropriate row and column numbers from the copies, and pass the copies as arguments to the recursive call. (Hopefully this description is specific enough to get you started thinking but vague enough to allow you to discover some things for yourself).
Example Interface code
To illustrate how the interface works, here is some code that could be used to test your method:
|
Running the above code should produce output something like this:
|