(1) | Table of Contents |
Crummett and Western, Physics: Models and Applications,
Sec.18-3,4
Halliday, Resnick, and Walker, Fundamentals of Physics (5th
ed.), Sec.19-6,7
Tipler, Physics for Scientists and Engineers (3rd ed.), Sec.
16-1,3
Materials differ from one another in the quantity of heat required to produce a given temperature change in a given mass of material. We define the heat capacity C of a sample of material as the heat input to cause unit temperature change,
(1)
and the specific heat capacity, c, as the heat capacity per unit mass:
(2)
c is
a property of a particular substance, approximately a constant if the temperature
change involved is not too large. Heat capacities are customarily measured
in terms of the calorie as energy unit; the definition of the calorie
is 
for water at
. Numerically 1
cal = 4.186 J.
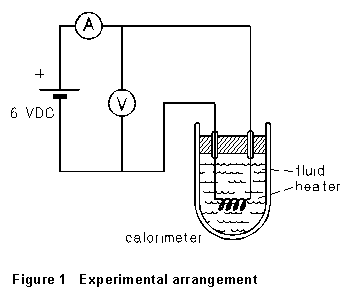
In this experiment, you're to measure the specific heat capacity of a liquid (a light machine oil). The experimental arrangement is sketched in Fig. 1. Heat is supplied by an electric heater to a sample of the fluid under observation, in an insulated vessel (the calorimeter). The rate at which heat is being supplied is known from the voltage and current to the heater, and the temperature of the liquid can be observed. We can write
(3)
provided all the input power goes to heating the calorimeter and its
contents -- that is, that there is no leakage of heat to
the surroundings. In Equation (3) c and m are the specific
heat capacity and the mass of the fluid being studied. 
is the aggregate heat capacity of the calorimeter, thermometer, stirrer,
and so forth (we may call this the "parasitic" heat capacity
of the system). From (3), then,
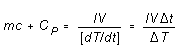(4)
where the rate of temperature increase, resulting from an input
power IV, is dT/dt. If the input power is constant over an
extended period 
,
the rate is equal to 
.
If the power supplied to the heater is constant, Equation (4) predicts
a uniform increase in temperature with time,
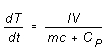(5)
In this case, a graph of temperature vs. time will be a straight line.
This conclusion is modified, however, if there is significant leakage of heat to the surroundings: if the insulation of the calorimeter vessel is not perfect, for example. Suppose the temperature of the surroundings is TS; then the rate at which heat is lost to the surroundings will be Y(T - TS), where Y is a constant reflecting the extent of the heat leak. Equation (3) would then turn into
and the equation for the rate of change of T as a function of t becomes
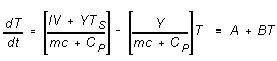(6)
in this case. Equation (6) is plainly equivalent to (5) if Y
= 0 (no heat leakage to the surroundings). If 
,
however, the slope of the temperature-time graph will decrease with
increasing temperature, because the rate of heat loss by conduction will
be higher at higher temperature; and if the slope is measured at two different
temperatures, we can calculate the heat loss constant Y from (6).
(1) Connect up the circuit indicated as in Figure 1. Current and voltage readings will be on the order of several amperes and several volts.
(2) Before determining the specific heat capacity of the oil,
you need to evaluate the parasitic heat capacity 
.
This will be done by using a liquid -- water -- whose specific heat is
known. Place 250 ml of distilled water in the thermos. Seal the thermos
and measure the temperature of the water. Then turn on the current
to the heater. Stir the liquid constantly by turning the glass thermometer;
a plastic stirrer is attached to its lower end.
At 1-minute intervals record temperature, voltage, and current readings in a single table. (You will probably find that voltage and current readings fluctuate slightly for the first few minutes but settle down to pretty stable equilibrium values after that.) At the end of 15 minutes, disconnect the power but keep stirring for a few minutes more to allow the system to come to thermal equilibrium. Record the final equilibrium temperature.
(3) Empty the calorimeter vessel and wipe it thoroughly dry. Place approximately 250 ml of transformer oil in the vessel and repeat the procedure of step (1).
(4) Determine the density of the oil by weighing a measured amount of it on the triple-beam balance.
(1) For your data on distilled water, calculate the average values
of voltage and current to the heater. Use Equation (4) to calculate the
parasitic heat capacity 
.
The final equilibrium temperature value should be used to calculate
, but 
is of course the length of time during which the current was on. Find the
standard error in your value of 
.
(2) Plot a graph of T vs. t for the distilled-water data.
You should obtain an essentially linear graph. Find the slope of the graph,
and use it in Equation (4) to calculate the parasitic heat capacity 
.
Find the uncertainty in this determination of 
.
Does this determination of 
agree, within experimental uncertainty, with that of step (1)? If you observe
a significant difference, how do you account for it? Which determination
do you consider the more reliable?
(3) For your data on transformer oil, calculate the average values
of voltage and current to the heater. Equation (4), together with the value
for 
you determined
above, can be used to determine the specific heat capacity of the oil.
The mass m is found from your measured density and known volume,
while 
and 
have the meanings discussed in step (1) above. Estimate the standard error
in your determination of c.
(4) Graph T vs. t for your data on transformer oil. Are the data adequately described by a straight-line graph, or is there significant curvature? A significant downward curvature probably arises from heat loss by conduction to the surroundings, as discussed in the paragraph around Equation (5). If you observe no significant curvature, use the slope of the graph in Equation (4) to determine the specific heat capacity c of the oil. If you do observe a curvature, then use the slope of the graph at the low-temperature end. (Not the average slope. Why not?) Does this determination of c agree, within experimental uncertainty, with that of step (3)?
(5) If, in step (4) above, you concluded that you are observing
significant heat loss by conduction, you can analyze your data in the following
way to estimate a value for the "heat conductance" Y in
Equation (5). From your T vs. t graph, estimate the slope dT/dt
at t = 0. In the same way, estimate dT/dt around t
= 5 min, t = 10 min, and t = 15 min. Use these values to
plot a graph of dT/dt vs. temperature; show your estimates of the
uncertainty in these values as error bars on the graph points. According
to Equation (5), this graph should be a straight line whose slope is 
.
From this, find Y, and estimate the error in this result. Watch
out for units!
(6) If, in step (4), you concluded that you are not observing significant conduction loss, try to estimate from your data an experimental upper limit on the value of Y.
Chapter 6 -- Other Experiments -- Conduction of Heat
last update 6/96