| Table of Contents |
Crummett and Western, Physics: Models and Applications,
Sec. 2.2, 3
Halliday, Resnick, and Walker, Fundamentals of Physics (5th
ed.), Sec. 3.1-3
Tipler, Physics for Scientists and Engineers (3rd ed.), Sec.
3.1, 2
A vector is a physical quantity which has both a magnitude and a direction in physical space. Force, for example, is a vector. Conventionally we represent a vector quantity in a diagram by an arrow in the appropriate direction, whose length represents the magnitude of the quantity. Vectors represent a new class of numbers, and they have their own rules of arithmetic. This experiment will let you examine the rule of vector addition, by directly adding forces.
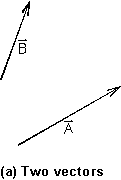
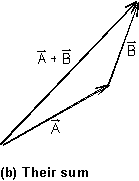The
diagram in Figure 1 defines the rule of vector addition. Take the two vectors
to be added; place them (graphically) nose to tail; the vector that connects
the beginning to the end of the chain is the sum, or resultant,
of the two vectors. The procedure can be generalized to any number of vectors
to be added. From the vector triangle in Figure 1, the law of cosines gives
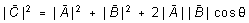(1)
If the addition of three or more vectors makes a closed polygon, the resultant of the vectors is zero. If the vectors represent forces, then the forces are in equilibrium. If
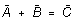
then plainly A, B, and the negative of C will always add to zero:
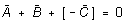
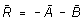(2)
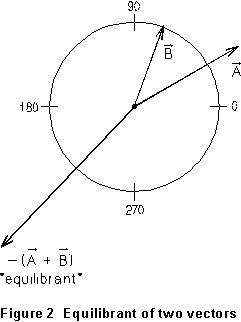
R is called the equilibrant of the system, because it is the vector which, added to A and B, brings the system into equilibrium. The equilibrant is always the negative of the sum of the other vectors. The two vectors and their equilibrant are sketched in Figure 2 below. This experiment uses a gadget called a force table, with which you measure the sum of two or more vectors by directly measuring their equilibrant.
A special case
of the addition of vectors that is very important to us is the resolution
of a vector into its components along orthogonal axes. In Figure , if is
the angle between A and the x axis, then
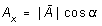(3a)
and 
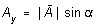(3b)
Any vector
is the equivalent of the vector sum of its components -- its projections
-- along any set of orthogonal (mutually perpendicular) coordinate axes;
Figure 2 makes clear that this is just the equivalence of the set of vectors
to their resultant.
It is usually to treat vector quantities analytically in terms of their components; for instance, addition of vectors is simply equivalent to ordinary scalar addition of thir corresponding components.
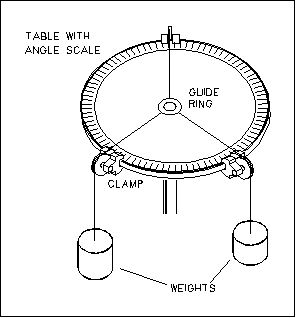The force table
is a circular table graduated in degrees from 0 degrees to 360 degrees
and provided with pulleys that can be set at any angles. Weights suspended
over the pulleys exert forces on the ring at the center, which is held
in place by a peg. When the ring is stable "off the peg," the
forces are in balance.
(1) Mount a pulley at the 20-degree mark on the force table and suspend a total of 200 g over it. Mount a second pulley at the 140-degree mark and suspend 100 g over it. In your notebook, draw a large, precise vector diagram like Figure 1a, and graphically determine the magnitude and direction of the resultant. Check yourself by calculating the resultant from Eq.(2).
(2) Find the equilibrant by setting up on the force table, by trial and error, a third force which balances the first two. Check to make sure that all the strings on the ring point directly at the center of the table. The resultant of the first two forces is the negative of the equilibrant. Does it agree with what you calculated, within experimental error?
(3) Use equations (3) to calculate the components of each of the first two forces and the equilibrant. Corresponding components should add to zero. Do they, within experimental error?
(4) Choose different values and angles for the first two weights, and repeat steps (1)-(3).
(5) Mount the first two pulleys as in Procedure (1), with the same weights at the same positions. Mount a third pulley at the 250-degree mark and suspend 150 g over it. Draw a vector diagram to scale and use it to determine graphically the resultant of the three vectors.
(6) Mount one pulley at the 30-degree mark and suspend a total of 200 g over it. Use Eqs. (3) to calculate its components along the x (0 degrees) and y (90 degrees) directions. Set up these two forces on the force table. These two forces, together, are equivalent to the original force. Reverse the first force by moving it 180 degrees, to 210 degrees. The three forces now on the table should be in balance. Are they?
GCK 6/96 - last update 7/97