| Table of Contents |
Crummett and Western, Physics: Models and Applications,
Sections 9-4,5
Halliday, Resnick, and Walker, Fundamentals of Physics (5th
ed.), Sec. 9-5,6
Tipler, Physics for Scientists and Engineers (3rd ed.), Sec.
7-3,6
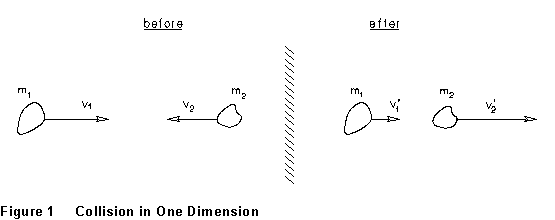
The theorem of conservation of linear momentum states that, if the vector sum of the external forces on a system of particles is zero, then the total linear momentum of the system remains constant, no matter what parts of the system may do. For a system of just two objects moving in one dimension, on which no net external force acts, this gives
(1)
where m1 and m2 are the masses of the two particles, v1 and v2 their respective velocities at some instant, and v1' and v2' the velocities at some other instant. (In Eq.(1), all v's are positive to the right -- in Figure 1, v2 would have a negative value.) In the case of a collision, v1 and v1' might be the velocities of object #1 just before and just after the collision, etc. Momentum conservation is particularly useful in collision-type situations, in which, typically, by far the most important forces are the internal forces that the two colliding objects exert on one another during the collision. Collision forces can frequently be assumed to be so strong that other forces, even if not zero, can be ignored just during the collision.
In an isolated system, momentum is conserved regardless of the nature of the forces of interaction. If these forces are conservative, mechanical energy as well as momentum will be conserved in the collision. Such an event is called a perfectly elastic collision. In a perfectly elastic collision, the relative speed of the two objects is the same before and after the collision:
(2)
Real collisions are not perfectly elastic. The "degree of elasticity"
of a collision is often expressed in terms of a quantity called the coefficient
of restitution 
of
the collision. 
is
defined as the ratio of the final to the initial relative speed of the
two colliding bodies:
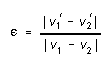(3)
can
never be greater than 1, and would be exactly 1 for a perfectly elastic
collision.
The opposite extreme would be a perfectly inelastic collision,
in which all the relative motion disappears: the two objects
stick together and move as one object after the collision.
For a perfectly inelastic collision, plainly, =
0.
If we adjust our focus to look at just one of the masses involved in a collision, another important theorem becomes apparent. The Impulse/Collision theorem states that there is a relationship between the net force exerted on the object and the change in the object's momentum:
(4)
Thus if one knows, or can measure the forces exerted on the object, the momentum change can be predicted.
This experiment has two parts. The first investigates two-cart collisions while the second investigates the collision of a single air cart with a strain gauge. Because of the small number of balances, there may be a bottleneck obtaining cart masses. If so, you can do the two-cart collision part of the experiment before you obtain masses, then later get the masses when a balance is free. For the strain gauge-impulse part of the experiment, you must have the cart mass before beginning, in order to calibrate the strain gauge properly. The sonic ranger must be calibrated by putting in the room temperature.
Run the program for taking simultaneous ranger and strain gauge data.
The strain gauge must be calibrated by leveling the air track and then
elevating the end near the strain gauge with the three aluminum shim blocks
provided. The air cart and its bumper with rubber bands is then placed
over the strain gauge aluminum bar so that the strain gauge bar is between
the rubber bands on the bumper, and the cart is restrained from sliding
down the track by one of the rubber bands in contact with the aluminum
bar of the strain gauge apparatus. One then goes to the 'Force Calibration'
Item on the anlsonic main menu, and selects 'Calibrate with mass in negative
F direction'. This calibration requires the mass in grams which
is applied to the strain gauge, assuming that the mass is hanging under
its own weight. For this calibration, the cart is on an air track which
is at an angle to the horizontal. You only want that fraction of the cart's
weight which is directed along the track: mgsin . The program automatically
adds the 'g', so you enter msin
for the mass. Then go to 'Preferences', then 'Analog Parameters', and set
up for channel B, -10v to +10v scale, and for 500 analog points taken at
a frequency of 500 Hz. Under 'Sonic Parameters', take 200 points. Check
that both 'IOBox' and 'mono' are selected.
Now remove the shims so the track is level again. In taking strain gauge data, start the ranger going as the cart approaches the strain gauge in mid-track. Just before the cart reaches the strain gauge, strike a key on the keyboard. This causes the sonic ranging to be interrupted, and a burst of strain gauge data to be taken for one second (500 points @ 500 Hz). Then the ranger resumes taking data and finishes. After this, you can look at the sonic data (x,t or v,t) or the force data. When you have some good data for force vs. time, save the data to file. The force graph should not 'max out' on top. This could happen if the cart had too much speed coming into the strain gauge. Show your lab instructor the force vs time plot for your first run before proceeding to make sure you are all right. One hard-copy F vs. t graph should be included in the report and analyzed. Do three trials.
Note: This program does not save the position vs. time data. You must extract the velocity values needed to calculate the momenta of the gliders for each run before you make another run or leave the program.
Get out of the ranger-strain gauge program and load the program for taking two-channel ranger data. In using two carts, put the cart with the smaller aluminum flag closer to the ranger. (Each cart should have only one flag on it - on the side facing the sonic ranger.) The sonic ranger should be pointed along the track at or above the height of the taller flag. Ask the lab instructor or the assistant to adjust if it's not behaving right.
Do three trials each of elastic collisions of equal-mass carts at unequal velocities and inelastic collision of unequal mass carts. Take data in tabular format. A sample format is shown here.
| Trial No. | v1i | v2i | v1f | v2f | Sv |
Estimating the velocity uncertainty: Estimate the uncertainty, Sv, in your measured velocities for each trial. You may estimate an uncertainty for each glider both before and after the collision( four Sv values per run), or you may want to make a single estimate which represents the uncertainty for all four velocities. Record the Sv value(s) in your data table along with the associated velocity values. If you choose to estimate the uncertainty in each individual cart velocity you will need to restructure the data table accordingly.
For the strain-gauge impulse work, the critical comparison is between the impulse from the (F,t) graph and the change in momentum from the sonic ranger data. The impulse exerted on the strain gauge by the cart should, in theory, equal the change in momentum of the cart. The analysis should include a simple graphical estimate of the total impulse during the collision. You will need to make a plot of F vs. T to do this. From the (x,t) data estimate the velocity of the cart before and after the collision. Calculate the change in momentum of the cart.
Error Analysis: Estimate the error in the impulse which you measured by your graphical estimate. Tell how you estimated this error. Does the impulse on the cart equal the change in momentum within this error? Comment on you result.
Momentum and impulse in collisions. Make a table showing the initial and final velocity and initial and final momentum of each cart, the total momentum before and after the collision, and the change in total momentum. There should be one line in the table for each two-cart collision. In general how does the total momentum of the two carts before each collision compare to the total momentum after the collision?
| Trial No. | Type of collision | p1i | p2i | p1f | p2f | Ptot,i | Ptot,f |
Kinetic energy in collisions. Make a table showing initial and final KE of each cart, total kinetic energy before the collision, and total kinetic energy after the collision for each two-cart collision. In general, how does the total kinetic energy before the collision compare with the total after the collision? Compare your observations with theory.
| Trial No. | Type of collision | KE1i | KE2i | KE1f | KE2f | KEtot,i | KEtot,f |
Error Analysis: Select a single elastic and a single inelastic collision and estimate the error in the total momentum before and after each collision. Is the total momentum conserved in each within estimated experimental error? If not, tell why you think momentum was not conserved. Do your observations conform with theory in each case?
For these same two collisions estimate the error in the total kinetic energy before and after each collision. Is the total kinetic energy conserved in each case within estimated experimental error? Do your observations conform with theory in each case?
last update DLH/MJM 7/97