 be
on the lookout for these.
be
on the lookout for these.| Table of Contents |
In discussing experimental errors, it's very useful to distinguish between systematic (sometimes called "determinate") and random ("indeterminate" or "chance" errors). Some sources of experimental error act to produce a bias in the result -- make the meter always read a little high, say; while others act to cause unpredictable fluctuations in the result -- make the meter read, unpredictably, a little different next time. The distinction is important because a systematic bias can't be revealed or assessed by repeating the measurement; if you try again, the same error happens again. On the other hand, once it's known, a source of systematic error can (at least in principle) be fixed or allowed for. Random fluctuations arise from unknown and unpredictable variations in conditions, and will produce a different error every time you try the experiment; but for just this reason you can assess their importance "internally," by trying the same experiment over and over and treating the results statistically. The basic concepts of such statistical error analysis are what the rest of this chapter is about; but don't forget that there may be systematic errors, to which statistics just don't apply, in any given experiment.
Then what can we do about systematic errors? Since a systematic error represents an intrinsic bias in the system consisting of the observer, his instruments, and his methods, the only way you can assess them is to vary the system. Some systematic errors are very easy to spot. Suppose you're measuring the thickness of something with a micrometer whose jaws are out of adjustment, so that it reads 0.06 mm rather than zero when the jaws are firmly closed. If the reading you get is 7.62 mm, you'd subtract the "zeroing error" and take the thickness as 7.56 mm. Most cases aren't this easy. If your meter stick is a cheaply made plastic one whose "millimeter" gradations are really 0.9962 mm apart, how are you going to tell? Using that meter stick, you aren't. You have to compare it to some precise standard, or use it to measure some previously known distance, or intercompare several different meter sticks of unrelated origin. Is your lab partner a little cross- eyed, so that he always reads the voltmeter one notch to the left of where it should be read? Compare readings made by several different observers. Are there contaminants in your instrumentation that are masking, or distorting, your results in a quantitative analysis? Run through all the steps of the experiment with a sample of known composition, or perhaps with no sample at all, and develop a correction to apply to your actual results. And so on. Ridding a given laboratory experiment of its systematic errors requires experience, imagination, and ingenuity.
Notice that if your experimental method itself is wrong, or ill-conceived,
or limited, this itself becomes a source of systematic error. In these
elementary lab experiments we won't (knowingly) give you any methods that
are downright wrong; but some of them do have definite limitations, and
you must always  be
on the lookout for these.
be
on the lookout for these.
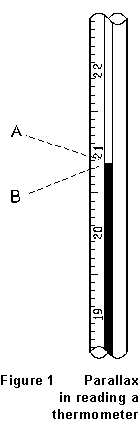
You should notice, too, that the distinction between systematic and random errors isn't always a hard and fast one. Consider the parallax error in reading a scale, as illustrated in Figure 1. The thermometer is "really" reading 20.87oC. An observer who repeatedly puts his eye at point A will read 20.94oC every time, so parallax has caused a systematic error of +0.07oC. But another observer who positions her eye carelessly, randomly, anywhere between A and B will read values that vary, randomly, from 20.79oC to 20.94oC. For this observer, parallax has been a source of random error. If she repeats her reading lots of times, and takes the average of the results, she'll end up with an answer that's closer to the true value; repeating measurements does nothing at all for the first experimenter.
(The "true value" has a rather specialized meaning in the context of statistical error analysis: it is the value that would be found by analyzing very large number of repeated trials of a measurement. That is, it may still include systematic errors, because statistical analysis won't help you identify these. When one says "true," the hedge "assuming there are no uncompensated systematic errors" is always to be understood.)
Properly used, the terms accuracy and precision reflect this distinction. A measurement with little systematic error -- thus one that will come close to the "right" answer -- has high accuracy; one with little random error -- thus one which is closely reproducible -- has high precision. In the example of Figure 1, the first observer made a precise measurement; the second made a less precise, but potentially more accurate, measurement.