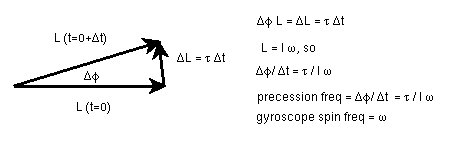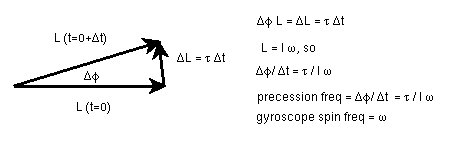Gyroscopic motion.

Recall that torque = dL/dt, so that dL = torque dt

There is a very large angular momentum vector L
This is due to a high angular velocity omega, and a sizable rotational inertia I
There is a torque on the gyro which changes L ( delta-L = torque delta-t )
The torque is perpendicular to L in the usual case, so delta-L is perpendicular to L
In a tiny amount of time delta-t, the tiny delta-L adds to L as shown in the sketch, not seriously changing its length
This means the L vector is rotated through a tiny angle delta-phi in a tiny time delta-t
The precession rate of the gyro is delta-phi over delta-t
The precession rate is connected to the angular velocity omega through the rotational inertia and the torque

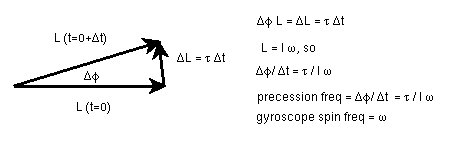
Activity with the bicycle wheel video (see resources page)

weight of the bicycle wheel is 29.5 N
length from supporting string to CM of wheel is 0.15 m
bike wheel Icm from the 50 g and 150 g masses is around 0.17 kg-m^2 (videos on resources page)
from the precessing bike wheel video (counting frame-by-frame)

Non-gyroscopic motion.

We hold a gyro at one end when it is not spinning and let the other end go.

Recall that torque = dL/dt, so that dL = torque dt

If the gyro is not spinning, it just falls over. Why?
The same torque acts as before
The torque is perpendicular to the axis of the gyro as before
delta-L is torque delta-t as before
but L=0 to begin with, so the tiny delta-L values just add together as time goes on
the non-spinning gyro begins to fall and its L value perpendicular to the plane of rotation increases
as the axis of the rotating (falling) gyro becomes vertical, its L is a maximum